《2025年课堂点睛九年级数学上册人教版安徽专版》

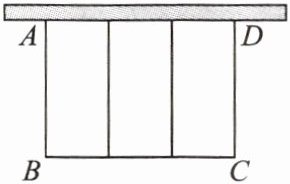
13. 如图,要利用一面墙(墙足够长)建羊圈,用 $100$ 米的围栏围成总面积为 $400$ 平方米的三个大小相同的矩形羊圈。设 $AB$ 长为 $x$ 米,则可列一般式方程为x²-25x+100=0。

答案： x²-25x+100=0

14. (分类讨论思想)若关于 $x$ 的方程 $x^{2}+(m + 1)x+\frac{1}{2}= 0$ 的一个实数根的倒数恰好是它本身,则 $m$ 的值是-5/2或1/2。(点拨：倒数等于本身的数有 $1$ 和 $-1$ 两个。)

答案： -5/2或1/2

15. 若关于 $x$ 的方程 $2mx(x - 1)-nx(x + 1)= 1$ 化成一般形式后为 $4x^{2}-2x - 1 = 0$,求 $m$,$n$ 的值。

答案： 解：整理方程得(2m-n)x²+(-2m-n)x-1=0，由题意得{2m-n=4,-2m-n=-2,解得{m=3/2,n=-1.

16. 已知 $m$ 是方程 $x^{2}-3x + 1 = 0$ 的一个根,求代数式 $(m - 2)^{2}+(m - 3)(m + 1)$ 的值。

答案： 解：把x=m代入方程，得m²-3m+1=0，
∴m²-3m=-1，
∴原式=m²-4m+4+m²-2m-3=2(m²-3m)+1=-1.

17. 根据下列问题,列出关于 $x$ 的方程,并将其化为一元二次方程的一般形式：
(1) 一个直角三角形的斜边长为 $10$,两条直角边相差 $2$,求较长的直角边长 $x$；
(2) $x$ 支球队参加篮球赛,参赛的每两支球队之间都要比赛一场,一共进行了 $15$ 场比赛,求参赛的篮球队支数 $x$。

答案： （1）解：x²+(x-2)²=100，一般形式为x²-2x-48=0. （2）1/2x(x-1)=15，一般形式为x²-x-30=0.

18. (核心素养·应用意识)一个三角形的两边长分别是 $2cm$ 和 $6cm$,第三条边长为 $a cm$。
(1) 求 $a$ 的取值范围；
(2) 若 $a$ 为整数,则 $a$ 的值有哪些？
(3) 若整数 $a$ 还满足方程 $a^{2}-9a + 14 = 0$,求此三角形的周长。

答案： （1）解：根据三角形三边关系得a的取值范围为4＜a＜8. （2）若a为整数，则a的值可为5或6或7. （3）当a=5时，a²-9a+14=-6；当a=6时，a²-9a+14=-4；当a=7时，a²-9a+14=0，
∴a的值为7.
∴三角形的周长为：2+6+7=15(cm).