《2025年课堂点睛九年级数学上册人教版安徽专版》

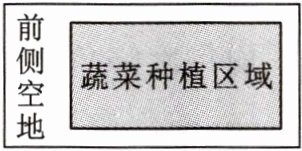
9. 某村计划建造如图所示的矩形蔬菜温室,要求长与宽的比为 2：1,在温室内,沿前侧内墙保留 3m 宽的空地,其他三侧内墙各保留 1m 的通道。当矩形温室的长与宽各为多少时,蔬菜种植区域的面积是$ 288m^2？$

答案： 解:设矩形温室的宽为xm,则长为2xm.根据题意,得(x −2)(2x−4)=288,整理得x²−4x−140=0,解得x₁=14,x₂=−10(不合题意,舍去),
∴x=14,2x=2×14=28.答:当矩形温室的长为28m,宽为14m时,蔬菜种植区域的面积是288m².

10. 关于 x 的一元二次方程 $x^2 + (a^2 - 2a)x + a - 1 = 0$ 的两个实数根互为相反数,则 a 的值为(B)
A.2
B.0
C.1
D.2 或 0

答案： B

11. 若关于 x 的一元二次方程 $(m - 1)x^2 + x + m^2 - 5m + 3 = 0$ 有一个根为 1,则 m 的值为3。

答案： 3

12. 已知关于 x 的一元二次方程 $x^2 - (2m + 1)x + m^2 + m = 0$。
(1)求证：无论 m 取何值,方程都有两个不相等的实数根；
(2)设该方程的两个实数根为 a,b,若 $(2a + b)(a + 2b) = 20$,求 m 的值。

答案：
(1)证明:
∵Δ=[-(2m+1)]²−4(m²+m)=4m²+4m+1−4m²−4m=1＞0,
∴无论m取何值，方程都有两个不相等的实数根.　
(2)解:
∵该方程的两个实数根为a,b,
∴a+b=-$\frac{-(2m+1)}{1}$=2m+1,ab=$\frac{m²+m}{1}$=m²+m.
∵(2a+b)(a+2b)=2a²+4ab+ab+2b²=2(a²+2ab+b²)+ab=2(a+b)²+ab,
∴2(a+b)²+ab =20.
∴2(2m+1)²+m²+m=20.解得m₁=−2,m₂=1.
∴m的值为−2或1.

13. 某商场销售一种玩具,每个成本 30 元,1 月份每个玩具售价 40 元,售出 100 个。为了提升销量,商场决定降价销售,据市场调查,该玩具的单价每下降 1 元(不能低于成本价),月销售量将增加 10 个。已知 3 月份销售额达到 5760 元。
(1)求 1 月份到 3 月份销售额的月平均增长率；
(2)求 3 月份时该玩具的销售价格。

答案：
(1)解:由题意，得1月份的销售额为40×100=4000(元).设1月份到3月份销售额的月平均增长率为x，得4000(1+x)²=5760,解得x₁=0.2=20%,x₂=−2.2(舍去).答:1月份到3月份销售额的月平均增长率为20%.　
(2)设3月份时,该玩具降价y元,由题意,得(40−y)(100+10y)=5760,整理得y²−30y+176=0,解得y₁=8,y₂=22,当y=22时,40−22=18＜30,不合题意,舍去;当y=8时,40−8=32＞30,符合题意.答:3月份时该玩具的销售价格为32元