第78页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
10. (原创题)已知平面直角坐标系内的三个点$A(1,-3)$,$B(0,-3)$,$C(2,-3)$,这三个点
不能
(填“能”或“不能”)确定一个圆。
答案:
不能
11. 如图,在$\triangle ABC$中,$\angle ACB= 90^{\circ}$,$AC= 4$,$BC= 5$,$M为AB$的中点。
(1)以点$C$为圆心,$4为半径作\odot C$,则点$A$、$B$、$M分别与\odot C$有怎样的位置关系?
(2)若以点$C为圆心作\odot C$,使$A$、$B$、$M三点中至少有一点在\odot C$内,且至少有一点在$\odot C$外,求$\odot C的半径r$的取值范围。
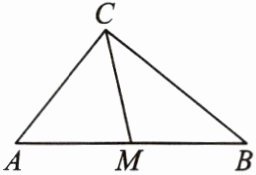
(1)以点$C$为圆心,$4为半径作\odot C$,则点$A$、$B$、$M分别与\odot C$有怎样的位置关系?
(2)若以点$C为圆心作\odot C$,使$A$、$B$、$M三点中至少有一点在\odot C$内,且至少有一点在$\odot C$外,求$\odot C的半径r$的取值范围。

答案:
(1)解:
∵在△ABC 中,∠ACB=90°,AC=4,BC=5,
∴AB=√(AC²+BC²)=√41.又
∵M 为 AB 的中点,
∴CM=(1/2)AB=(√41)/2.
∵以点 C 为圆心,4 为半径作⊙C,AC=4,
∴点 A 在⊙C 上.
∵CM=(√41)/2<4,
∴点 M 在⊙C 内.
∵BC=5>4,
∴点 B 在⊙C 外.
(2)以点 C 为圆心作⊙C,当 A、B、M 三点中至少有一点在⊙C 内时,r>(√41)/2.至少有一点在⊙C 外时,r<5.故⊙C 的半径 r 的取值范围为(√41)/2<r<5.
(1)解:
∵在△ABC 中,∠ACB=90°,AC=4,BC=5,
∴AB=√(AC²+BC²)=√41.又
∵M 为 AB 的中点,
∴CM=(1/2)AB=(√41)/2.
∵以点 C 为圆心,4 为半径作⊙C,AC=4,
∴点 A 在⊙C 上.
∵CM=(√41)/2<4,
∴点 M 在⊙C 内.
∵BC=5>4,
∴点 B 在⊙C 外.
(2)以点 C 为圆心作⊙C,当 A、B、M 三点中至少有一点在⊙C 内时,r>(√41)/2.至少有一点在⊙C 外时,r<5.故⊙C 的半径 r 的取值范围为(√41)/2<r<5.
12. 如图所示,要把破残的圆片复制完整。已知弧上的三点$A$,$B$,$C$。
(1)用尺规作图法找出$\overset{\frown}{BC}$所在圆的圆心;(保留作图痕迹,不写作法)
(2)设$\triangle ABC$是等腰三角形,底边$BC= 8cm$,腰$AB= 5cm$。求圆片的半径$R$。
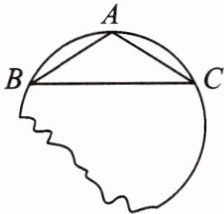
(1)用尺规作图法找出$\overset{\frown}{BC}$所在圆的圆心;(保留作图痕迹,不写作法)
(2)设$\triangle ABC$是等腰三角形,底边$BC= 8cm$,腰$AB= 5cm$。求圆片的半径$R$。

答案:
(1)解:分别作 AB,AC 的垂直平分线,设交点为 O,则 O 为所求圆的圆心.
(2)连接 AO 交 BC 于点 E.
∵AB=AC,
∴AE⊥BC,BE=(1/2)BC=4cm.在 Rt△ABE 中,AE=√(AB²-BE²)=√(5²-4²)=3(cm).连接 OB,在 Rt△BEO 中,OB²=BE²+OE²,即 R²=4²+(R-3)²,解得 R=25/6cm.即所求圆片的半径为25/6cm.
(1)解:分别作 AB,AC 的垂直平分线,设交点为 O,则 O 为所求圆的圆心.
(2)连接 AO 交 BC 于点 E.
∵AB=AC,
∴AE⊥BC,BE=(1/2)BC=4cm.在 Rt△ABE 中,AE=√(AB²-BE²)=√(5²-4²)=3(cm).连接 OB,在 Rt△BEO 中,OB²=BE²+OE²,即 R²=4²+(R-3)²,解得 R=25/6cm.即所求圆片的半径为25/6cm.
13. (核心素养·抽象能力)如图,$AD为\triangle ABC$外接圆的直径,$AD\perp BC于点F$,$\angle ABC的平分线交AD于点E$,连接$BD$,$CD$。
(1)求证:$BD= CD$;
(2)请判断$B$,$E$,$C三点是否在以点D$为圆心,以$DB$为半径的圆上,并说明理由。
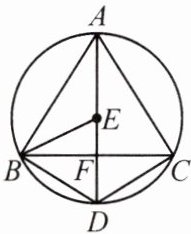
(1)求证:$BD= CD$;
(2)请判断$B$,$E$,$C三点是否在以点D$为圆心,以$DB$为半径的圆上,并说明理由。

答案:
(1)证明:
∵AD 为圆的直径,AD⊥BC,
∴弧 BD=弧 CD,
∴BD=CD.
(2)解:B,E,C 三点在以 D 为圆心,以 DB 为半径的圆上.理由如下:
∵BE 平分∠ABC,
∴∠ABE=∠EBF.
∵∠BED=∠BAD+∠ABE,∠EBD=∠EBF+∠CBD,∠CBD=∠CAD=∠BAD,
∴∠BED=∠EBD,
∴DE=DB.又
∵DB=DC,
∴DB=DE=DC,
∴B,E,C 三点在以点 D 为圆心,以 DB 为半径的圆上.
(1)证明:
∵AD 为圆的直径,AD⊥BC,
∴弧 BD=弧 CD,
∴BD=CD.
(2)解:B,E,C 三点在以 D 为圆心,以 DB 为半径的圆上.理由如下:
∵BE 平分∠ABC,
∴∠ABE=∠EBF.
∵∠BED=∠BAD+∠ABE,∠EBD=∠EBF+∠CBD,∠CBD=∠CAD=∠BAD,
∴∠BED=∠EBD,
∴DE=DB.又
∵DB=DC,
∴DB=DE=DC,
∴B,E,C 三点在以点 D 为圆心,以 DB 为半径的圆上.
查看更多完整答案,请扫码查看


