第59页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
1. 下列各选项中的两个图形成中心对称的是(

C
)
答案:
C
2. 如图,已知△ABC 和△DEF 关于点 O 对称,则 AO =
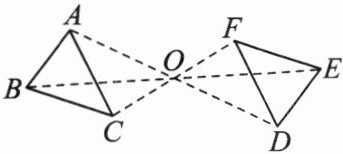
DO
,BO = EO
,CO = FO
.点 A 关于对称中心 O 的对称点是点D
,点 B 关于对称中心 O 的对称点是点E
,点 C 关于对称中心 O 的对称点是点F
.
答案:
DO EO FO 点D 点E 点F
3.(教材第 66 页第 1 题变式)如图,在方格图中,已知格点△ABC 和点 O,画△A'B'C'和△ABC 关于点 O 成中心对称.
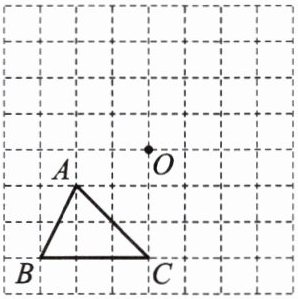

答案:
解:如图所示
解:如图所示

4.(新考法)如图所示的 4 组图形中,左边图形与右边图形是中心对称图形的是
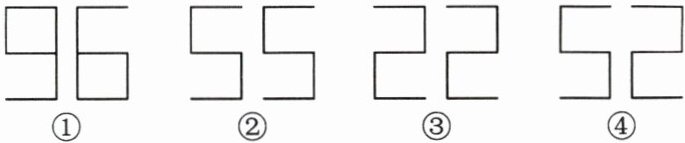
①②③
.
答案:
①②③
5.(原创题)如图,正方形 ABCD 与正方形 GHEF 成中心对称,则下列关于对称中心的描述不正确的是(

A.对称中心是线段 CE 的中点
B.对称中心是线段 DF 的中点
C.对称中心是点 E
D.对称中心是线段 AG 与 DF 的交点
C
)
A.对称中心是线段 CE 的中点
B.对称中心是线段 DF 的中点
C.对称中心是点 E
D.对称中心是线段 AG 与 DF 的交点
答案:
C
6. 如图,直线 a、b 垂直相交于点 O,曲线 C 关于点 O 成中心对称,点 A 的对称点是点 A',AB⊥a 于点 B,A'D⊥b 于点 D.若 OB = 3,OD = 2,则阴影部分的面积之和为
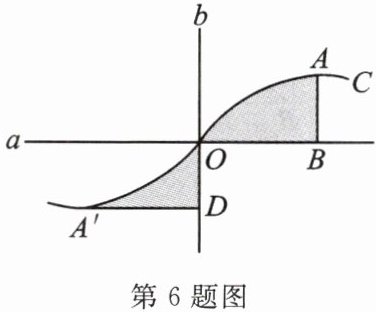
6
.
答案:
6
7.(核心素养·应用意识)如图,正方形 ABCD 与正方形 A'B'C'D'关于点 O 成中心对称.若正方形 ABCD 的边长为 1,设图形重合部分的面积为 y,线段 OB 的长为 x.
(1)当 x = 1 时,线段 OD 的长为
(2)求 y 与 x 之间的函数关系式.
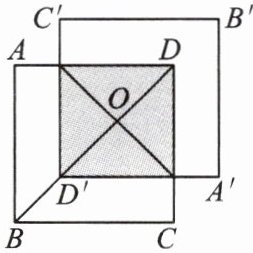
(1)当 x = 1 时,线段 OD 的长为
$\sqrt{2}-1$
;(2)求 y 与 x 之间的函数关系式.

解:设 CD 与$A'D'$交于点 E,AD 与$C'D'$交于点 F.
∵正方形 ABCD 与正方形$A'B'C'D'$关于点 O 成中心对称,
∴四边形$DED'F$是正方形.
∵正方形 ABCD 的边长为 1,
∴$BD=\sqrt{2}$.
∵$OB=x$,
∴$OD = BD - OB=\sqrt{2}-x$.
∴$DE=\sqrt{2}(\sqrt{2}-x)=2-\sqrt{2}x$.
∴$y = S_{正方形DED'F}=DE^{2}=(2-\sqrt{2}x)^{2}=2x^{2}-4\sqrt{2}x + 4$.
∴y 与 x 之间的函数关系式为$y = 2x^{2}-4\sqrt{2}x + 4$.
∵正方形 ABCD 与正方形$A'B'C'D'$关于点 O 成中心对称,
∴四边形$DED'F$是正方形.
∵正方形 ABCD 的边长为 1,
∴$BD=\sqrt{2}$.
∵$OB=x$,
∴$OD = BD - OB=\sqrt{2}-x$.
∴$DE=\sqrt{2}(\sqrt{2}-x)=2-\sqrt{2}x$.
∴$y = S_{正方形DED'F}=DE^{2}=(2-\sqrt{2}x)^{2}=2x^{2}-4\sqrt{2}x + 4$.
∴y 与 x 之间的函数关系式为$y = 2x^{2}-4\sqrt{2}x + 4$.
答案:
(1)$\sqrt{2}-1$
(2)解:设 CD 与$A'D'$交于点 E,AD 与$C'D'$交于点 F.
∵正方形 ABCD 与正方形$A'B'C'D'$关于点 O 成中心对称,
∴四边形$DED'F$是正方形.
∵正方形 ABCD 的边长为 1,
∴$BD=\sqrt{2}$.
∵$OB=x$,
∴$OD = BD - OB=\sqrt{2}-x$.
∴$DE=\sqrt{2}(\sqrt{2}-x)=2-\sqrt{2}x$.
∴$y = S_{正方形DED'F}=DE^{2}=(2-\sqrt{2}x)^{2}=2x^{2}-4\sqrt{2}x + 4$.
∴y 与 x 之间的函数关系式为$y = 2x^{2}-4\sqrt{2}x + 4$.
(1)$\sqrt{2}-1$
(2)解:设 CD 与$A'D'$交于点 E,AD 与$C'D'$交于点 F.
∵正方形 ABCD 与正方形$A'B'C'D'$关于点 O 成中心对称,
∴四边形$DED'F$是正方形.
∵正方形 ABCD 的边长为 1,
∴$BD=\sqrt{2}$.
∵$OB=x$,
∴$OD = BD - OB=\sqrt{2}-x$.
∴$DE=\sqrt{2}(\sqrt{2}-x)=2-\sqrt{2}x$.
∴$y = S_{正方形DED'F}=DE^{2}=(2-\sqrt{2}x)^{2}=2x^{2}-4\sqrt{2}x + 4$.
∴y 与 x 之间的函数关系式为$y = 2x^{2}-4\sqrt{2}x + 4$.
查看更多完整答案,请扫码查看


