第71页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
1. 下列图形中的角是圆心角的是 (
]
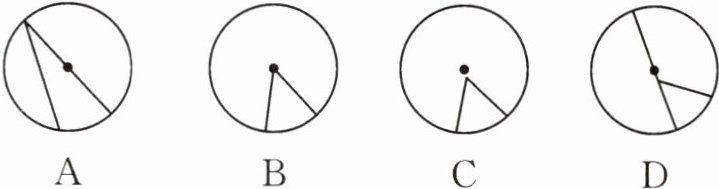
B
)]

答案:
B
2. 如图,已知 $ AB $ 为 $ \odot O $ 的直径,点 $ D $ 为半圆周上的一点,且 $ \overset{\frown}{AD} $ 所对圆心角的度数是 $ \overset{\frown}{BD} $ 所对圆心角度数的 $ 2 $ 倍,则圆心角 $ \angle BOD = $
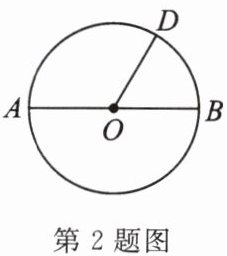
$60°$
.
答案:
$60°$
3. 如图所示,在 $ \odot O $ 中,若 $ C $ 是 $ \overset{\frown}{AB} $ 的中点, $ \angle AOC = 45^{\circ} $,则 $ \angle AOB $ 等于 (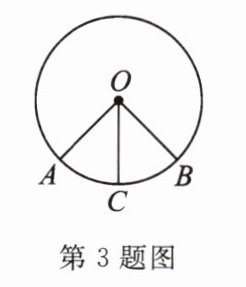
A.$ 45^{\circ} $
B.$ 80^{\circ} $
C.$ 85^{\circ} $
D.$ 90^{\circ} $
D
)
A.$ 45^{\circ} $
B.$ 80^{\circ} $
C.$ 85^{\circ} $
D.$ 90^{\circ} $
答案:
D
4. (教材第 $ 85 $ 页第 $ 2 $ 题变式)如图, $ AB $ 是 $ \odot O $ 的直径, $ \overset{\frown}{BC} = \overset{\frown}{CD} = \overset{\frown}{DE} $, $ \angle BOC = 40^{\circ} $,则 $ \angle AOE = $ ______
60°
.zyjl.cn/pic18/2025-09-19/07cf4ef93f7c7ade534cf4e6140ffde3.jpg?x-oss-process=image/crop,x_280,y_1866,w_221,h_266">
答案:
$60°$
5. 如图, $ \odot O $ 中, $ \overset{\frown}{AB} = \overset{\frown}{AC} $, $ \angle A = 30^{\circ} $,则 $ \angle C = $
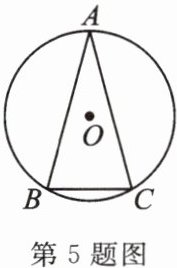
75
$ ^{\circ} $.
答案:
75
6. 如图,在 $ \odot O $ 中, $ AB = CD $,求证: $ AD = BC $.
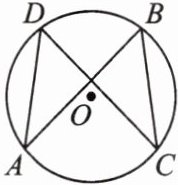

答案:
证明:$\because AB=CD$,$\therefore \overset{\frown}{ADB}=\overset{\frown}{CBD}$,$\therefore \overset{\frown}{ADB}-\overset{\frown}{BD}=\overset{\frown}{CBD}-\overset{\frown}{BD}$,即$\overset{\frown}{AD}=\overset{\frown}{BC}$,$\therefore AD=BC$。
7. 如图, $ AB $ 是 $ \odot O $ 的直径,点 $ C $ 在 $ \odot O $ 上, $ \angle AOC = 40^{\circ} $, $ D $ 是 $ \overset{\frown}{BC} $ 的中点,求 $ \angle OCD $ 的度数.


答案:
解:连接 $OD$,$\because D$ 是$\overset{\frown}{BC}$的中点,$\therefore \overset{\frown}{CD}=\overset{\frown}{BD}$。$\therefore \angle COD=\angle BOD=\frac{1}{2}\angle BOC$。$\because \angle AOC=40°$,$AB$ 是$\odot O$的直径,$\therefore \angle BOC=180° - 40°=140°$。$\therefore \angle COD=\frac{1}{2}×140°=70°$。又$\because OC=OD$,$\therefore \angle OCD=\frac{1}{2}×(180° - 70°)=55°$。
8. 如图,若 $ \overset{\frown}{AB} $ 和 $ \overset{\frown}{AC} $ 是同圆的两条弧,且 $ \overset{\frown}{AB} = 2 \overset{\frown}{AC} $,那么弦 $ AB $ 与 $ 2AC $ 的大小关系是 (
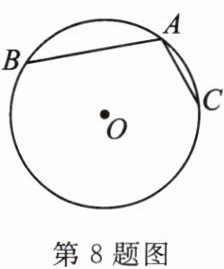
A.$ AB = 2AC $
B.$ AB < 2AC $
C.$ AB > 2AC $
D.无法确定
B
)
A.$ AB = 2AC $
B.$ AB < 2AC $
C.$ AB > 2AC $
D.无法确定
答案:
B
【变式】如图,在 $ \odot O $ 中,若 $ \angle AOB = 2 \angle COD $,则下列结论正确的是 (

A.$ \overset{\frown}{AB} > 2 \overset{\frown}{CD} $
B.$ \overset{\frown}{AB} = 2 \overset{\frown}{CD} $
C.$ \overset{\frown}{AB} < 2 \overset{\frown}{CD} $
D.以上都不对
B
)
A.$ \overset{\frown}{AB} > 2 \overset{\frown}{CD} $
B.$ \overset{\frown}{AB} = 2 \overset{\frown}{CD} $
C.$ \overset{\frown}{AB} < 2 \overset{\frown}{CD} $
D.以上都不对
答案:
B
9. 如图, $ AB $ 是 $ \odot O $ 的直径, $ \angle BOD = 120^{\circ} $,点 $ C $ 为弧 $ BD $ 的中点, $ AC $ 交 $ OD $ 于点 $ E $, $ DE = 1 $,则 $ AE $ 的长为 (

A.$ \sqrt{3} $
B.$ \sqrt{5} $
C.$ 2 \sqrt{3} $
D.$ 2 \sqrt{5} $
A
)
A.$ \sqrt{3} $
B.$ \sqrt{5} $
C.$ 2 \sqrt{3} $
D.$ 2 \sqrt{5} $
答案:
A
查看更多完整答案,请扫码查看


