第49页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
1. (锦州市中考)某文具店购进一批单价为12元的学习用品,按照相关部门规定其销售单价不低于进价,且不高于进价的1.5倍,通过分析销售情况,发现每天的销售量y(件)与销售单价x(元)满足一次函数关系,且当$x = 15$时,$y = 50$;当$x = 17$时,$y = 30$。
(1) 则y与x之间的函数关系式是
(2) 这种学习用品的销售单价定为多少时,每天可获得最大利润?最大利润是多少元?
(1) 则y与x之间的函数关系式是
$ y=-10x+200 $
;(2) 这种学习用品的销售单价定为多少时,每天可获得最大利润?最大利润是多少元?
解:设每天获得的利润为$ w $元,由(1)可得:$ w=(x-12)(-10x+200)=-10x^2+320x-2400=-10(x-16)^2+160 $,∵$ 12 \leqslant x \leqslant 18 $,且$ -10<0 $,∴开口向下,∴当$ x=16 $时,$ w $有最大值,最大值为 160.答:这种学习用品的销售单价定为 16 元时,每天可获得最大利润,最大利润是 160 元.
答案:
(1)$ y=-10x+200 $
(2)解:设每天获得的利润为$ w $元,由
(1)可得:$ w=(x-12)(-10x+200)=-10x^2+320x-2400=-10(x-16)^2+160 $,
∵$ 12 \leqslant x \leqslant 18 $,且$ -10<0 $,
∴开口向下,
∴当$ x=16 $时,$ w $有最大值,最大值为 160.答:这种学习用品的销售单价定为 16 元时,每天可获得最大利润,最大利润是 160 元.
(1)$ y=-10x+200 $
(2)解:设每天获得的利润为$ w $元,由
(1)可得:$ w=(x-12)(-10x+200)=-10x^2+320x-2400=-10(x-16)^2+160 $,
∵$ 12 \leqslant x \leqslant 18 $,且$ -10<0 $,
∴开口向下,
∴当$ x=16 $时,$ w $有最大值,最大值为 160.答:这种学习用品的销售单价定为 16 元时,每天可获得最大利润,最大利润是 160 元.
2. 某小区业主委员会决定把一块长50m、宽30m的矩形空地建成健身广场,设计方案如图所示,阴影区域为绿化区(四块绿化区为全等的矩形),空白区域为活动区,且四周的4个出口宽度相同,其宽度不小于14m、不大于26m。设绿化区较长边为xm,活动区的面积为$ym^2$。
(1) ① 用含x的式子表示出口的宽度为
② 写出y与x的函数关系式及x的取值范围:
(2) 求活动区的面积y的最大值。
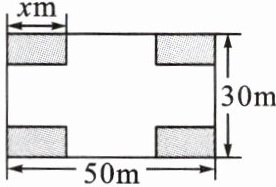
(1) ① 用含x的式子表示出口的宽度为
50-2x
m;② 写出y与x的函数关系式及x的取值范围:
$ y=-4x^2+40x+1500(12 \leqslant x \leqslant 18) $
;(2) 求活动区的面积y的最大值。

答案:
(1)①$ 50-2x $ ②$ y=-4x^2+40x+1500(12 \leqslant x \leqslant 18) $
(2)解:$ y=-4x^2+40x+1500=-4(x-5)^2+1600 $.
∵$ -4<0 $,对称轴为直线$ x=5 $,
∴当$ 12 \leqslant x \leqslant 18 $时,$ y $随$ x $的增大而减小,
∴当$ x=12 $时,$ y_{最大}=1404 $.答:活动区的面积$ y $的最大值为$ 1404m^2 $.
(1)①$ 50-2x $ ②$ y=-4x^2+40x+1500(12 \leqslant x \leqslant 18) $
(2)解:$ y=-4x^2+40x+1500=-4(x-5)^2+1600 $.
∵$ -4<0 $,对称轴为直线$ x=5 $,
∴当$ 12 \leqslant x \leqslant 18 $时,$ y $随$ x $的增大而减小,
∴当$ x=12 $时,$ y_{最大}=1404 $.答:活动区的面积$ y $的最大值为$ 1404m^2 $.
3. (丹东市中考)丹东是我国的边境城市,拥有丰富的旅游资源。某景区研发一款纪念品,每件成本为30元,投放景区内进行销售,规定销售单价不低于成本且不高于54元,销售一段时间调研发现,每天的销售数量y(件)与销售单价x(元/件)满足一次函数关系,部分数据如下表所示:
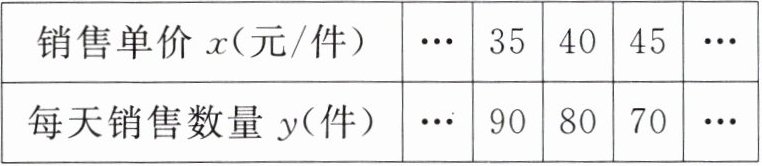
(1) 则y与x的函数关系式是
(2) 当销售单价为多少元时,每天获利最大?最大利润是多少元?

(1) 则y与x的函数关系式是
$ y=-2x+160 $
;(2) 当销售单价为多少元时,每天获利最大?最大利润是多少元?
答案:
(1)$ y=-2x+160 $
(2)解:设每天获利$ w $元,$ w=(x-30)·(-2x+160)=-2x^2+220x-4800=-2(x-55)^2+1250 $,
∵$ -2<0 $,对称轴是直线$ x=55 $,当$ x \leqslant 55 $时,$ w $随$ x $的增大而增大.
∵$ x \leqslant 54 $,
∴$ x=54 $时,$ w $取最大值,最大值是$ -2×(54-55)^2+1250=1248 $(元).答:当销售单价为 54 元时,每天获利最大,最大利润是 1248 元.
(1)$ y=-2x+160 $
(2)解:设每天获利$ w $元,$ w=(x-30)·(-2x+160)=-2x^2+220x-4800=-2(x-55)^2+1250 $,
∵$ -2<0 $,对称轴是直线$ x=55 $,当$ x \leqslant 55 $时,$ w $随$ x $的增大而增大.
∵$ x \leqslant 54 $,
∴$ x=54 $时,$ w $取最大值,最大值是$ -2×(54-55)^2+1250=1248 $(元).答:当销售单价为 54 元时,每天获利最大,最大利润是 1248 元.
4. 某工厂生产销售A,B两种型号车床共14台,生产并销售1台A型车床可以获利10万元;如果生产并销售不超过4台B型车床,则每台B型车床可以获利17万元,如果超过4台B型车床,则每超出1台,每台B型车床获利将均减少1万元。设生产并销售B型车床x台。
(1) 当$x > 4$时,完成以下两个问题:
① 请补全下面的表格:
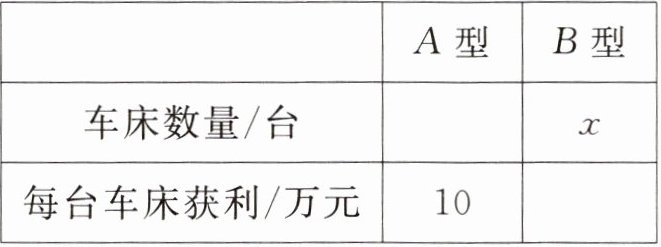
② 若生产并销售B型车床比生产并销售A型车床获得的利润多70万元,则生产并销售B型车床
(2) 当$0 < x \leq 14$时,设生产并销售A,B两种型号车床获得的总利润为W万元,如何分配生产并销售A,B两种车床的数量,使获得的总利润W最大?并求出最大利润。
(1) 当$x > 4$时,完成以下两个问题:
① 请补全下面的表格:

② 若生产并销售B型车床比生产并销售A型车床获得的利润多70万元,则生产并销售B型车床
10
台。(2) 当$0 < x \leq 14$时,设生产并销售A,B两种型号车床获得的总利润为W万元,如何分配生产并销售A,B两种车床的数量,使获得的总利润W最大?并求出最大利润。
解:当$ 0<x \leqslant 4 $时,$ W=10(14-x)+17x $,整理,得$ W=7x+140 $.
∵$ 7>0 $,
∴当$ x=4 $时总利润$ W $最大,最大利润为$ 7×4+140=168 $(万元);当$ 4<x \leqslant 14 $时,$ W=10(14-x)+(21-x)x $,整理,得$ W=-x^2+11x+140 $.
∵$ -1<0 $,
∴当$ x=-\frac{11}{2×(-1)}=5.5 $时总利润$ W $最大.又由题意知$ x $只能取整数,
∴当$ x=5 $或$ x=6 $时,总利润$ W $最大.
∴当$ x=5 $时,最大利润为$ -5^2+11×5+140=170 $(万元).又
∵$ 168<170 $,
∴当$ x=5 $或$ x=6 $时,总利润$ W $最大.又
∵$ 14-5=9 $(台),$ 14-6=8 $(台),
∴当生产并销售A,B两种车床各为 9 台、5 台或 8 台、6 台时,获得的总利润$ W $最大,最大利润为170 万元.
∵$ 7>0 $,
∴当$ x=4 $时总利润$ W $最大,最大利润为$ 7×4+140=168 $(万元);当$ 4<x \leqslant 14 $时,$ W=10(14-x)+(21-x)x $,整理,得$ W=-x^2+11x+140 $.
∵$ -1<0 $,
∴当$ x=-\frac{11}{2×(-1)}=5.5 $时总利润$ W $最大.又由题意知$ x $只能取整数,
∴当$ x=5 $或$ x=6 $时,总利润$ W $最大.
∴当$ x=5 $时,最大利润为$ -5^2+11×5+140=170 $(万元).又
∵$ 168<170 $,
∴当$ x=5 $或$ x=6 $时,总利润$ W $最大.又
∵$ 14-5=9 $(台),$ 14-6=8 $(台),
∴当生产并销售A,B两种车床各为 9 台、5 台或 8 台、6 台时,获得的总利润$ W $最大,最大利润为170 万元.
答案:
(1)①$ 14-x $ $ 21-x $ ②10
(2)解:当$ 0<x \leqslant 4 $时,$ W=10(14-x)+17x $,整理,得$ W=7x+140 $.
∵$ 7>0 $,
∴当$ x=4 $时总利润$ W $最大,最大利润为$ 7×4+140=168 $(万元);当$ 4<x \leqslant 14 $时,$ W=10(14-x)+(21-x)x $,整理,得$ W=-x^2+11x+140 $.
∵$ -1<0 $,
∴当$ x=-\frac{11}{2×(-1)}=5.5 $时总利润$ W $最大.又由题意知$ x $只能取整数,
∴当$ x=5 $或$ x=6 $时,总利润$ W $最大.
∴当$ x=5 $时,最大利润为$ -5^2+11×5+140=170 $(万元).又
∵$ 168<170 $,
∴当$ x=5 $或$ x=6 $时,总利润$ W $最大.又
∵$ 14-5=9 $(台),$ 14-6=8 $(台),
∴当生产并销售A,B两种车床各为 9 台、5 台或 8 台、6 台时,获得的总利润$ W $最大,最大利润为170 万元.
(1)①$ 14-x $ $ 21-x $ ②10
(2)解:当$ 0<x \leqslant 4 $时,$ W=10(14-x)+17x $,整理,得$ W=7x+140 $.
∵$ 7>0 $,
∴当$ x=4 $时总利润$ W $最大,最大利润为$ 7×4+140=168 $(万元);当$ 4<x \leqslant 14 $时,$ W=10(14-x)+(21-x)x $,整理,得$ W=-x^2+11x+140 $.
∵$ -1<0 $,
∴当$ x=-\frac{11}{2×(-1)}=5.5 $时总利润$ W $最大.又由题意知$ x $只能取整数,
∴当$ x=5 $或$ x=6 $时,总利润$ W $最大.
∴当$ x=5 $时,最大利润为$ -5^2+11×5+140=170 $(万元).又
∵$ 168<170 $,
∴当$ x=5 $或$ x=6 $时,总利润$ W $最大.又
∵$ 14-5=9 $(台),$ 14-6=8 $(台),
∴当生产并销售A,B两种车床各为 9 台、5 台或 8 台、6 台时,获得的总利润$ W $最大,最大利润为170 万元.
查看更多完整答案,请扫码查看


