第72页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
19. 在三角形纸片ABC中,∠C= 90°,AC= BC= 8,要在三角形纸片ABC中剪出一个扇形,使过扇形的弧两端的半径都在三角形纸片ABC的边上,且扇形的弧与三角形纸片ABC的其他边相切.
(1) 画出所有符合题意的设计方案示意图.
(2) 若用剪下的扇形围成圆锥的侧面,求相应圆锥的底面半径.
(3) 你所设计的方案中,方案______所围成的圆锥侧面积最小,方案______所围成的圆锥侧面积相等,等于______.
解:(1) 方案如下:
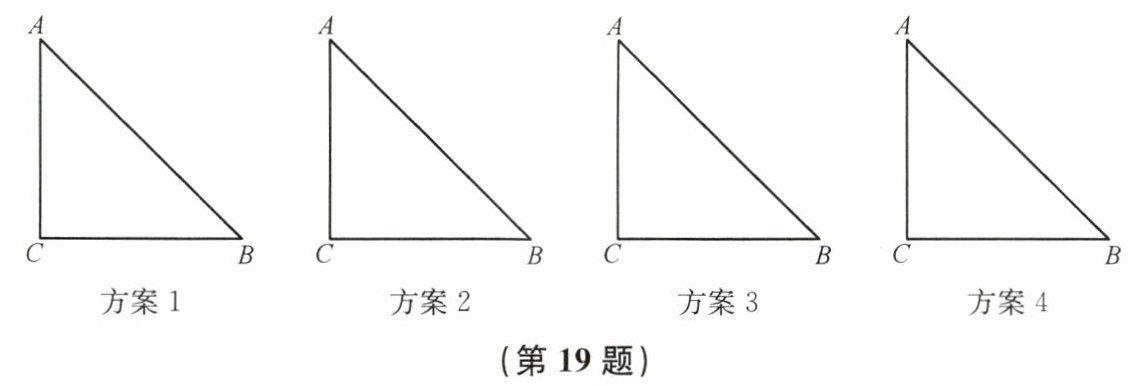
(1) 画出所有符合题意的设计方案示意图.
(2) 若用剪下的扇形围成圆锥的侧面,求相应圆锥的底面半径.
(3) 你所设计的方案中,方案______所围成的圆锥侧面积最小,方案______所围成的圆锥侧面积相等,等于______.
解:(1) 方案如下:

答案:
1,4
8π
2,3
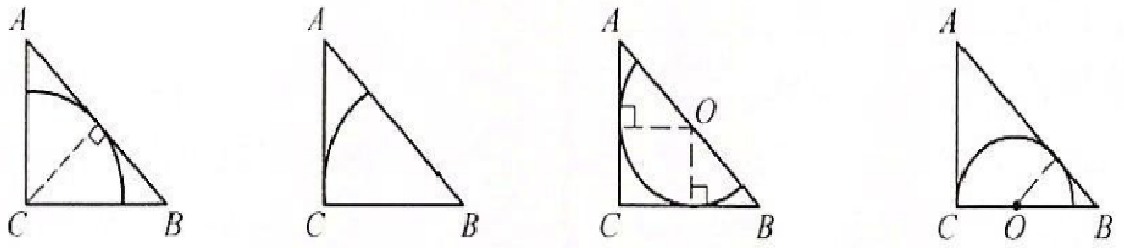
解:
(2)设圆锥的底面半径为r
在方案1中
∵AC=BC,∠ACB=90°
∴扇形的半径为$\frac {1}{2}AB=\frac {1}{2}\sqrt{8^2+ 8^2}=4\sqrt{2}$
∵圆心角为90°
∴$2πr=\frac { 90π×4\sqrt{2}}{180},$
∴$r=\sqrt{2}$
在方案2中
∵构成扇形的半径为8,圆心角为45°
∴$2πr=\frac { 45π×8}{ 180} $
∴r=1
在方案3中
∵扇形的圆心在斜边AB上,此时四边形
OMCN为正方形
∴ON=CN
∵在Rt△ONA中,∠A=45°
∴ON=NA
∴$ON=\frac {1}{2}AC=4$
∴2πr=4π
∴r=2
在方案4中
∵扇形的圆心角在BC边上,是以O为圆心的半
圆,设OC=OM=R
在Rt△OMB中,∠B=45°
∴OM=MB
∴$OB=\sqrt{2}R$
∵OC+OB=BC
∴$R+\sqrt{2}R=8$
∴$R=8\sqrt{2}-8$
∴$2πr=π(8\sqrt{2}-8)$
∴$r=4\sqrt{ 2}-4$
综上,剪下的扇形所围成的圆锥的底面半径为
$\sqrt{2}$或1或2或$4\sqrt{2}-4$
1,4
8π
2,3

解:
(2)设圆锥的底面半径为r
在方案1中
∵AC=BC,∠ACB=90°
∴扇形的半径为$\frac {1}{2}AB=\frac {1}{2}\sqrt{8^2+ 8^2}=4\sqrt{2}$
∵圆心角为90°
∴$2πr=\frac { 90π×4\sqrt{2}}{180},$
∴$r=\sqrt{2}$
在方案2中
∵构成扇形的半径为8,圆心角为45°
∴$2πr=\frac { 45π×8}{ 180} $
∴r=1
在方案3中
∵扇形的圆心在斜边AB上,此时四边形
OMCN为正方形
∴ON=CN
∵在Rt△ONA中,∠A=45°
∴ON=NA
∴$ON=\frac {1}{2}AC=4$
∴2πr=4π
∴r=2
在方案4中
∵扇形的圆心角在BC边上,是以O为圆心的半
圆,设OC=OM=R
在Rt△OMB中,∠B=45°
∴OM=MB
∴$OB=\sqrt{2}R$
∵OC+OB=BC
∴$R+\sqrt{2}R=8$
∴$R=8\sqrt{2}-8$
∴$2πr=π(8\sqrt{2}-8)$
∴$r=4\sqrt{ 2}-4$
综上,剪下的扇形所围成的圆锥的底面半径为
$\sqrt{2}$或1或2或$4\sqrt{2}-4$
20. 一走廊拐角的横截面如图所示,已知AB⊥BC,AB//DE,BC//FG,且两组平行墙壁间的走廊宽度都是1 m,$\widehat{EF}$所在圆的圆心为O,半径为1 m,∠EOF= 90°,DE、FG分别与$\widehat{EF}$所在的⊙O相切于点E、F. 若水平放置的木棒MN的两个端点M、N分别在AB和BC上,且MN与⊙O相切于点P,P是$\widehat{EF}$的中点,求木棒MN的长度.
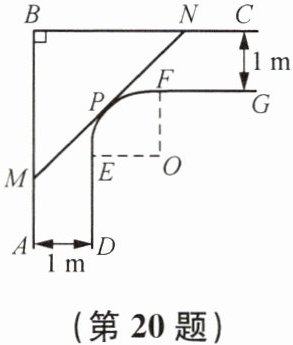

答案:
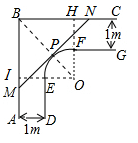
解:连接OB,延长OF,OE分别交BC于H,交
AB于I
∵DE、FG分别与⊙O相切于E、F两点
∴OE⊥ED,OF⊥FG
∵AB//DE,BC//FG
∴OI⊥AB,OH⊥BC
∵∠EOF=90°
∴四边形BIOH是矩形
∵两组平行墙壁间的走廊宽度都是1m,⊙O半径为1m
∴OI=OH=2
∴矩形BIOH是正方形
∴∠OBI=∠OBH=45°
∵P是$\widehat{EF}$的中点
∴OB经过P点
在正方形BIOH中,边长=2
∴$OB=2\sqrt{2}$
∵OP=1
∴$BP=2\sqrt{2}-1$
∵P是MN与⊙O的切点
∴OB⊥MN
∵∠OBI=∠OBH=45°,OB⊥MN
∴MP=NP=BP
∴MN=2BP
∵$BP=2\sqrt{2}-1$
∴$MN=2(2\sqrt{2}-1)=4\sqrt{2}-2$

解:连接OB,延长OF,OE分别交BC于H,交
AB于I
∵DE、FG分别与⊙O相切于E、F两点
∴OE⊥ED,OF⊥FG
∵AB//DE,BC//FG
∴OI⊥AB,OH⊥BC
∵∠EOF=90°
∴四边形BIOH是矩形
∵两组平行墙壁间的走廊宽度都是1m,⊙O半径为1m
∴OI=OH=2
∴矩形BIOH是正方形
∴∠OBI=∠OBH=45°
∵P是$\widehat{EF}$的中点
∴OB经过P点
在正方形BIOH中,边长=2
∴$OB=2\sqrt{2}$
∵OP=1
∴$BP=2\sqrt{2}-1$
∵P是MN与⊙O的切点
∴OB⊥MN
∵∠OBI=∠OBH=45°,OB⊥MN
∴MP=NP=BP
∴MN=2BP
∵$BP=2\sqrt{2}-1$
∴$MN=2(2\sqrt{2}-1)=4\sqrt{2}-2$
查看更多完整答案,请扫码查看


