第108页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
练习
1. 若点A(x₁,y₁)、B(x₂,y₂)、C(x₃,y₃)在反比例函数$y= \frac{3}{x}$的图像上,且$x₁<x₂<0<x₃$,则y₁、y₂、y₃的大小关系是(
$A.y_3>y_1>y_2$
$B.y_1>y_2>y_3$
$C.y_2>y_1>y_3$
$D.y_3>y_2>y_1$
1. 若点A(x₁,y₁)、B(x₂,y₂)、C(x₃,y₃)在反比例函数$y= \frac{3}{x}$的图像上,且$x₁<x₂<0<x₃$,则y₁、y₂、y₃的大小关系是(
A
).$A.y_3>y_1>y_2$
$B.y_1>y_2>y_3$
$C.y_2>y_1>y_3$
$D.y_3>y_2>y_1$
答案:
解:
∵反比例函数$y=\frac{3}{x}$中,$k=3>0$,
∴函数图像在第一、三象限,在每个象限内,$y$随$x$的增大而减小。
∵点$A(x_1,y_1)$、$B(x_2,y_2)$、$C(x_3,y_3)$在该函数图像上,且$x_1<x_2<0<x_3$,
∴点$A$、$B$在第三象限,点$C$在第一象限。
∴$y_1<0$,$y_2<0$,$y_3>0$。
∵在第三象限内,$y$随$x$的增大而减小,且$x_1<x_2$,
∴$y_1>y_2$。
综上,$y_3>y_1>y_2$。
答案:A
∵反比例函数$y=\frac{3}{x}$中,$k=3>0$,
∴函数图像在第一、三象限,在每个象限内,$y$随$x$的增大而减小。
∵点$A(x_1,y_1)$、$B(x_2,y_2)$、$C(x_3,y_3)$在该函数图像上,且$x_1<x_2<0<x_3$,
∴点$A$、$B$在第三象限,点$C$在第一象限。
∴$y_1<0$,$y_2<0$,$y_3>0$。
∵在第三象限内,$y$随$x$的增大而减小,且$x_1<x_2$,
∴$y_1>y_2$。
综上,$y_3>y_1>y_2$。
答案:A
2. 已知函数$y= \frac{1}{x}$的图像如图所示. 当$x≥-1$时,y的取值范围是(
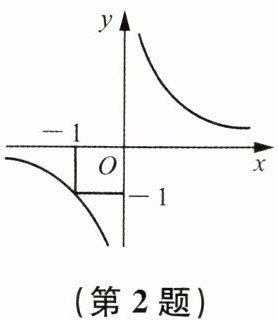
A.y≤-1
B.y≤-1和y≥0
C.y≤-1和y>0
D.y<-1和y≥0
C
).
A.y≤-1
B.y≤-1和y≥0
C.y≤-1和y>0
D.y<-1和y≥0
答案:
【解析】:本题考查数形结合思想,需要根据给定的$x$的取值范围,结合反比例函数$y = \frac{1}{x}$的图像来确定$y$的取值范围。
已知函数$y = \frac{1}{x}$,这是一个反比例函数,其图像在第一、三象限。
当$x\geq - 1$时,分两种情况讨论:
当$-1\leq x\lt 0$时:
对于反比例函数$y = \frac{1}{x}$,此时$y=\frac{1}{-1\leq x\lt 0}$,根据反比例函数的性质,当$x$为负数且绝对值越来越小时,$y$的值会越来越小且为负数。
当$x = - 1$时,$y=\frac{1}{-1}=-1$,所以当$-1\lt x\lt 0$时,$y\lt - 1$,结合$x = - 1$时$y = - 1$,可得当$-1\leq x\lt 0$时,$y\leq - 1$。
当$x\gt 0$时:
对于反比例函数$y = \frac{1}{x}$,此时$y=\frac{1}{x\gt 0}$,根据反比例函数的性质,当$x$为正数且越来越大时,$y$的值会越来越小且为正数,但始终大于$0$,即$y\gt 0$。
综合以上两种情况,当$x\geq - 1$时,$y$的取值范围是$y\leq - 1$和$y\gt 0$。
【答案】:C。
已知函数$y = \frac{1}{x}$,这是一个反比例函数,其图像在第一、三象限。
当$x\geq - 1$时,分两种情况讨论:
当$-1\leq x\lt 0$时:
对于反比例函数$y = \frac{1}{x}$,此时$y=\frac{1}{-1\leq x\lt 0}$,根据反比例函数的性质,当$x$为负数且绝对值越来越小时,$y$的值会越来越小且为负数。
当$x = - 1$时,$y=\frac{1}{-1}=-1$,所以当$-1\lt x\lt 0$时,$y\lt - 1$,结合$x = - 1$时$y = - 1$,可得当$-1\leq x\lt 0$时,$y\leq - 1$。
当$x\gt 0$时:
对于反比例函数$y = \frac{1}{x}$,此时$y=\frac{1}{x\gt 0}$,根据反比例函数的性质,当$x$为正数且越来越大时,$y$的值会越来越小且为正数,但始终大于$0$,即$y\gt 0$。
综合以上两种情况,当$x\geq - 1$时,$y$的取值范围是$y\leq - 1$和$y\gt 0$。
【答案】:C。
3. 如图,一次函数$y= kx+b$的图像经过点A(-1,-2)和点B(-2,0),正比例函数$y= 2x$的图像经过点A. 则不等式$2x<kx+b<0$的解集为(
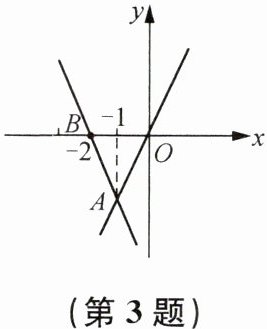
A.x<-2
B.-2<x<-1
C.-2<x<0
D.-1<x<0
B
).
A.x<-2
B.-2<x<-1
C.-2<x<0
D.-1<x<0
答案:
【解析】:本题可根据一次函数与正比例函数的图像性质,结合不等式$2x<kx + b<0$,通过分析函数图像的位置关系来求解不等式的解集。
步骤一:分析$2x<kx + b$的解集
$2x<kx + b$表示正比例函数$y = 2x$的图像在一次函数$y = kx + b$图像的下方。
已知正比例函数$y = 2x$的图像经过点$A(-1,-2)$,一次函数$y = kx + b$的图像经过点$A(-1,-2)$和点$B(-2,0)$。
从图像上看,当$x< -1$时,正比例函数$y = 2x$的图像在一次函数$y = kx + b$图像的下方,所以$2x<kx + b$的解集为$x< -1$。
步骤二:分析$kx + b<0$的解集
$kx + b<0$表示一次函数$y = kx + b$的图像在$x$轴下方。
因为一次函数$y = kx + b$的图像经过点$B(-2,0)$,从图像上看,当$x> -2$时,一次函数$y = kx + b$的图像在$x$轴下方,所以$kx + b<0$的解集为$x> -2$。
步骤三:求不等式$2x<kx + b<0$的解集
综合以上两个不等式的解集,取它们的交集,即同时满足$2x<kx + b$和$kx + b<0$的$x$的取值范围。
所以不等式$2x<kx + b<0$的解集为$-2<x< -1$。
【答案】:B
步骤一:分析$2x<kx + b$的解集
$2x<kx + b$表示正比例函数$y = 2x$的图像在一次函数$y = kx + b$图像的下方。
已知正比例函数$y = 2x$的图像经过点$A(-1,-2)$,一次函数$y = kx + b$的图像经过点$A(-1,-2)$和点$B(-2,0)$。
从图像上看,当$x< -1$时,正比例函数$y = 2x$的图像在一次函数$y = kx + b$图像的下方,所以$2x<kx + b$的解集为$x< -1$。
步骤二:分析$kx + b<0$的解集
$kx + b<0$表示一次函数$y = kx + b$的图像在$x$轴下方。
因为一次函数$y = kx + b$的图像经过点$B(-2,0)$,从图像上看,当$x> -2$时,一次函数$y = kx + b$的图像在$x$轴下方,所以$kx + b<0$的解集为$x> -2$。
步骤三:求不等式$2x<kx + b<0$的解集
综合以上两个不等式的解集,取它们的交集,即同时满足$2x<kx + b$和$kx + b<0$的$x$的取值范围。
所以不等式$2x<kx + b<0$的解集为$-2<x< -1$。
【答案】:B
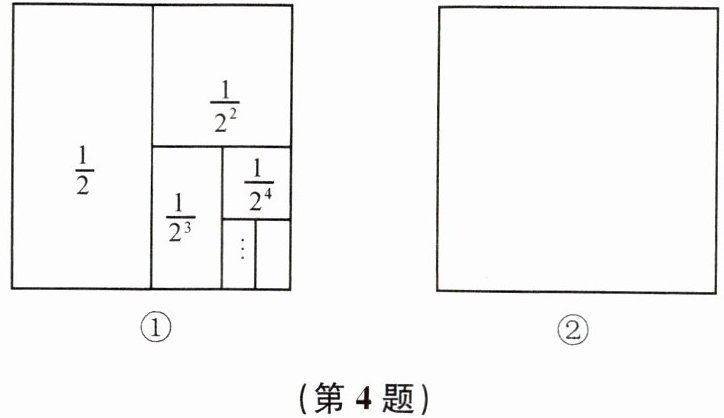
4. 在数学活动中,小明为了求$\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+\frac{1}{2^4}+...+\frac{1}{2^n}$的值(结果用n表示),设计了如图①的几何图形. 于是,有$\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+\frac{1}{2^4}+...+\frac{1}{2^n}= $______. 请你利用图②,再设计一个能求$\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+\frac{1}{2^4}+...+\frac{1}{2^n}$的值的几何图形.

答案:
解:$1 - \frac{1}{2^n}$
设计几何图形如下:
将图②的正方形看作单位“1”。
第一次将正方形沿水平方向平均分成2份,取其中一份为$\frac{1}{2}$;
第二次将剩余的$\frac{1}{2}$部分沿垂直方向平均分成2份,取其中一份为$\frac{1}{2^2}$;
第三次将剩余的$\frac{1}{2^2}$部分沿水平方向平均分成2份,取其中一份为$\frac{1}{2^3}$;
以此类推,经过n次分割后,所取各部分面积之和即为$\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+\cdots+\frac{1}{2^n}$,此时剩余部分面积为$\frac{1}{2^n}$,所以所求和为$1 - \frac{1}{2^n}$。
设计几何图形如下:
将图②的正方形看作单位“1”。
第一次将正方形沿水平方向平均分成2份,取其中一份为$\frac{1}{2}$;
第二次将剩余的$\frac{1}{2}$部分沿垂直方向平均分成2份,取其中一份为$\frac{1}{2^2}$;
第三次将剩余的$\frac{1}{2^2}$部分沿水平方向平均分成2份,取其中一份为$\frac{1}{2^3}$;
以此类推,经过n次分割后,所取各部分面积之和即为$\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+\cdots+\frac{1}{2^n}$,此时剩余部分面积为$\frac{1}{2^n}$,所以所求和为$1 - \frac{1}{2^n}$。
查看更多完整答案,请扫码查看


