《2025年同步练习江苏九年级数学上册苏科版》

16. 某学校向园林公司购买了一批树苗. 园林公司规定：如果购买树苗不超过60棵,每棵售价120元；如果购买树苗超过60棵,每增加1棵,所出售的这批树苗每棵售价均降低0.5元,但每棵树苗售价不得低于100元. 该学校最终支付园林公司树苗款8800元,购买的树苗有多少棵？

答案： 解：因为60棵树苗售价为120×60=7200元$\lt $
8800元，所以该校购买树苗超过60棵，设该校
共购买了x棵树苗，由题意得：
x[120-0.5(x-60)]=8800
解得： {x}_{1}=220， {x}_{2}=80
当x=220时
$120-0.5×(220-60)=40\lt 100$
所以x=220(不合题意，舍去)
当x=80时
$120-0.5×(80-60)=110\gt 100$
所以x=80
答：该校共购买了80棵树苗。

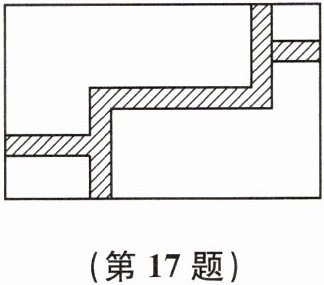
17. 如图,在宽20 m、长32 m的矩形地面上修建等宽的道路(图中阴影部分),余下的部分种上草坪,要使草坪的面积为$540 m^2,$求道路的宽.
]

答案： 解：设道路的宽度是xm
根据题意可得方程：(32-x)(20-x)=540
整理得：x^{2}-52x+100=0
解得：$ {x}_1=2，$$ {x}_2=50($不合题意舍去)
答：道路的宽度是2m。

18. 有下列关于$x$的方程：①$x^2+px+n= 0$；②$x^2+mx+q= 0$. 已知方程①的两个根是1和$m+1$,方程②的两个根是2和$n-1$,解方程：$x^2+px+q= 0$.

答案： 解：根据题意得1+m+1＝-p①
$1\cdot (m+1)＝n②$
2+n-1＝-m③
2(n-1)＝q④
由②③解得m＝-1，n＝0
所以p＝-1，q＝-2
则方程x^{2}+px+q＝0变形为方程
x^{2}-x-2＝0
(x-2)(x+1)＝0
所以$ {x}_1＝2，$$ {x}_2＝-1$

19. 某商场经营某种品牌的玩具,购进时的单价是30元. 根据市场调查：在一段时间内,销售单价是40元时,销售量是600件；销售单价每涨1元,就会少售出10件玩具. 设该玩具的销售单价定为$x$元,商场能获得的销售利润为$w$元.
(1)用含$x的代数式表示w$.
(2)该玩具的销售单价定为多少元时,商场能获得12000元的销售利润？
(3)该玩具的销售单价定为多少元时,商场获得的销售利润最大？最大利润是多少？

答案： 解：
(1)根据题意得w=(x-30)[600-10(x-40)]
(2)(x-30)[600-10(x-40)]=12000
解得$x_1=60，$$x_2=70$
答：玩具销售单价为60元或70元时，可获得12000元销售利润。
$ (3)w=(x-30)[600-10(x-40)]=-10x^2+1300x-30000=-10(x-65)^2+12250$

∴当x=65时，w_{最大}=12250
答：当该玩具销售单价为65元时，商场获得最大利润12250元。