第109页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
例2 已知a、b为正数,且a+b= 2,求$\sqrt{4+a^2}+\sqrt{1+b^2}$的最小值.
点评:此题由式子特点联想勾股定理,构造图形解决问题.
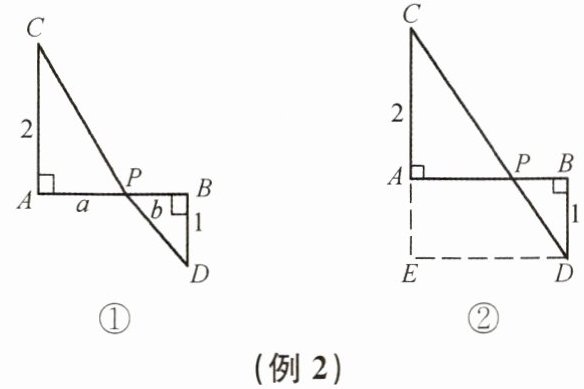
解:如图①,作线段AB= 2,在AB上取点P,设AP= a,则BP= b. 作AC⊥AB,且取AC= 2,作BD⊥AB,且取BD= 1. 由勾股定理,得$PC= \sqrt{4+a^2}$,$PD= \sqrt{1+b^2}$. 当点P与点C、D在同一直线上时,PC+PD的值最小,即为线段CD的长.
如图②,作AB= 2,AC⊥AB、BD⊥AB,且取AC= 2、BD= 1,作DE//BA交CA的延长线于点E. 在Rt△CDE中,CE= CA+AE= 2+1= 3,DE= AB= 2,$CD= \sqrt{CE^2+DE^2}= \sqrt{3^2+2^2}= \sqrt{13}$,即$\sqrt{4+a^2}+\sqrt{1+b^2}的最小值是\sqrt{13}$.
点评:此题由式子特点联想勾股定理,构造图形解决问题.
解:如图①,作线段AB= 2,在AB上取点P,设AP= a,则BP= b. 作AC⊥AB,且取AC= 2,作BD⊥AB,且取BD= 1. 由勾股定理,得$PC= \sqrt{4+a^2}$,$PD= \sqrt{1+b^2}$. 当点P与点C、D在同一直线上时,PC+PD的值最小,即为线段CD的长.
如图②,作AB= 2,AC⊥AB、BD⊥AB,且取AC= 2、BD= 1,作DE//BA交CA的延长线于点E. 在Rt△CDE中,CE= CA+AE= 2+1= 3,DE= AB= 2,$CD= \sqrt{CE^2+DE^2}= \sqrt{3^2+2^2}= \sqrt{13}$,即$\sqrt{4+a^2}+\sqrt{1+b^2}的最小值是\sqrt{13}$.

答案:
【解析】:
本题主要考查了勾股定理以及数形结合的数学思想。
首先,根据题目条件,已知$a+b=2$,且$a$、$b$为正数。
接着,为了求解$\sqrt{4+a^2}+\sqrt{1+b^2}$的最小值,可以构造一个图形,其中线段$AB$的长度为2,$AP$的长度为$a$,$BP$的长度为$b$。
然后,分别作$AC$垂直于$AB$且长度为2,$BD$垂直于$AB$且长度为1。
根据勾股定理,可以计算出$PC$和$PD$的长度,分别为$\sqrt{4+a^2}$和$\sqrt{1+b^2}$。
当点$P$与点$C$、$D$在同一直线上时,$PC+PD$的值最小,即等于线段$CD$的长度。
为了求出$CD$的长度,可以再构造一个与图形相关的直角三角形。
作$DE$平行于$BA$交$CA$的延长线于点$E$,这样$DE$的长度就等于$AB$的长度,即2;
$CE$的长度等于$CA$与$AE$的和,即3。
最后,利用勾股定理求出$CD$的长度,即$\sqrt{3^2+2^2}=\sqrt{13}$。
所以,$\sqrt{4+a^2}+\sqrt{1+b^2}$的最小值为$\sqrt{13}$。
【答案】:
$\sqrt{13}$。
本题主要考查了勾股定理以及数形结合的数学思想。
首先,根据题目条件,已知$a+b=2$,且$a$、$b$为正数。
接着,为了求解$\sqrt{4+a^2}+\sqrt{1+b^2}$的最小值,可以构造一个图形,其中线段$AB$的长度为2,$AP$的长度为$a$,$BP$的长度为$b$。
然后,分别作$AC$垂直于$AB$且长度为2,$BD$垂直于$AB$且长度为1。
根据勾股定理,可以计算出$PC$和$PD$的长度,分别为$\sqrt{4+a^2}$和$\sqrt{1+b^2}$。
当点$P$与点$C$、$D$在同一直线上时,$PC+PD$的值最小,即等于线段$CD$的长度。
为了求出$CD$的长度,可以再构造一个与图形相关的直角三角形。
作$DE$平行于$BA$交$CA$的延长线于点$E$,这样$DE$的长度就等于$AB$的长度,即2;
$CE$的长度等于$CA$与$AE$的和,即3。
最后,利用勾股定理求出$CD$的长度,即$\sqrt{3^2+2^2}=\sqrt{13}$。
所以,$\sqrt{4+a^2}+\sqrt{1+b^2}$的最小值为$\sqrt{13}$。
【答案】:
$\sqrt{13}$。
5. 若关于x的不等式组$\begin{cases}2x<3(x-3)+1 \\ \frac{3x+2}{4}>x+a\end{cases} $有4个整数解,则a的取值范围是
$-\frac{11}{4} \leq a < -\frac{5}{2}$
.
答案:
解:解不等式$2x < 3(x - 3) + 1$,得$x > 8$。
解不等式$\frac{3x + 2}{4} > x + a$,得$x < 2 - 4a$。
所以不等式组的解集为$8 < x < 2 - 4a$。
因为不等式组有4个整数解,即9,10,11,12,所以$12 < 2 - 4a \leq 13$。
解得$-\frac{11}{4} \leq a < -\frac{5}{2}$。
$-\frac{11}{4} \leq a < -\frac{5}{2}$
解不等式$\frac{3x + 2}{4} > x + a$,得$x < 2 - 4a$。
所以不等式组的解集为$8 < x < 2 - 4a$。
因为不等式组有4个整数解,即9,10,11,12,所以$12 < 2 - 4a \leq 13$。
解得$-\frac{11}{4} \leq a < -\frac{5}{2}$。
$-\frac{11}{4} \leq a < -\frac{5}{2}$
6. 在平面直角坐标系中直接画出函数$y= |x|$的图像. 若一次函数$y= kx+b$的图像分别过点A(-1,1)、B(2,2),根据这两个函数的图像写出方程组$\begin{cases}y= |x| \\ y= kx+b\end{cases} $的解.
答案:
解:函数$y = |x|$的图像如图所示:
(此处因无法直接画图,实际答题时需在坐标系中画出第一、二象限的角平分线)
设一次函数$y = kx + b$,将$A(-1,1)$、$B(2,2)$代入得:
$\begin{cases}-k + b = 1 \\ 2k + b = 2\end{cases}$
解得$\begin{cases}k = \dfrac{1}{3} \\ b = \dfrac{4}{3}\end{cases}$,所以一次函数解析式为$y = \dfrac{1}{3}x + \dfrac{4}{3}$。
联立$\begin{cases}y = |x| \\ y = \dfrac{1}{3}x + \dfrac{4}{3}\end{cases}$
当$x \geq 0$时,$x = \dfrac{1}{3}x + \dfrac{4}{3}$,解得$x = 2$,$y = 2$;
当$x < 0$时,$-x = \dfrac{1}{3}x + \dfrac{4}{3}$,解得$x = -1$,$y = 1$。
所以方程组的解为$\begin{cases}x=-1 \\ y=1\end{cases}$,$\begin{cases}x=2 \\ y=2\end{cases}$。
(此处因无法直接画图,实际答题时需在坐标系中画出第一、二象限的角平分线)
设一次函数$y = kx + b$,将$A(-1,1)$、$B(2,2)$代入得:
$\begin{cases}-k + b = 1 \\ 2k + b = 2\end{cases}$
解得$\begin{cases}k = \dfrac{1}{3} \\ b = \dfrac{4}{3}\end{cases}$,所以一次函数解析式为$y = \dfrac{1}{3}x + \dfrac{4}{3}$。
联立$\begin{cases}y = |x| \\ y = \dfrac{1}{3}x + \dfrac{4}{3}\end{cases}$
当$x \geq 0$时,$x = \dfrac{1}{3}x + \dfrac{4}{3}$,解得$x = 2$,$y = 2$;
当$x < 0$时,$-x = \dfrac{1}{3}x + \dfrac{4}{3}$,解得$x = -1$,$y = 1$。
所以方程组的解为$\begin{cases}x=-1 \\ y=1\end{cases}$,$\begin{cases}x=2 \\ y=2\end{cases}$。
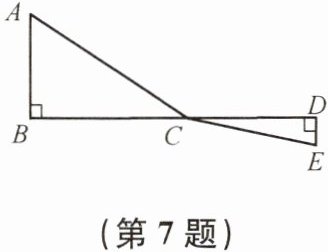
7. 如图,C为线段BD上一动点,分别过点B、D作AB⊥BD、ED⊥BD,连接AC、EC. 已知AB= 5,DE= 1,BD= 8,设CD= x.
(1) 用含x的代数式表示AC+CE的长;
(2) 求AC+CE的最小值;
(3) 根据(2)中的规律和结论,请构图求出代数式$\sqrt{x^2+4}+\sqrt{(12-x)^2+9}$的最小值.
(1) 用含x的代数式表示AC+CE的长;
(2) 求AC+CE的最小值;
(3) 根据(2)中的规律和结论,请构图求出代数式$\sqrt{x^2+4}+\sqrt{(12-x)^2+9}$的最小值.

答案:
(1) 解:因为 BD=8,CD=x,所以 BC=BD-CD=8-x。
因为 AB⊥BD,AB=5,所以在 Rt△ABC 中,AC=$\sqrt{AB^2 + BC^2}=\sqrt{5^2+(8-x)^2}=\sqrt{(8-x)^2 + 25}$。
因为 ED⊥BD,DE=1,所以在 Rt△CDE 中,CE=$\sqrt{CD^2 + DE^2}=\sqrt{x^2 + 1^2}=\sqrt{x^2 + 1}$。
所以 AC+CE=$\sqrt{(8 - x)^2 + 25}+\sqrt{x^2 + 1}$。
(2) 解:作点 A 关于直线 BD 的对称点 A',连接 A'E 交 BD 于点 C,此时 AC+CE 的值最小,最小值为 A'E 的长。
因为点 A 与 A'关于 BD 对称,AB=5,所以 A'B=AB=5,∠A'BD=∠ABD=90°,所以 A',B,D 三点共线,且 A'D=A'B + BD=5 + 8=13?(此处错误,应为 A'在 AB 延长线上,A'B=AB=5,所以 A'到 D 的水平距离为 BD=8,垂直距离为 A'B + DE=5 + 1=6?不,重新构建:过点 A'作 A'F⊥ED 交 ED 的延长线于点 F。
则 A'F=BD=8,EF=DE + A'B=1 + 5=6。
在 Rt△A'FE 中,A'E=$\sqrt{A'F^2 + EF^2}=\sqrt{8^2 + 6^2}=\sqrt{64 + 36}=\sqrt{100}=10$。
所以 AC+CE 的最小值为 10。
(3) 解:构造直角梯形,使上底为 2,下底为 3,高为 12。设梯形的下底左端点为 B,右端点为 D,上底左端点为 A,右端点为 E,AB⊥BD,DE⊥BD,AB=2,DE=3,BD=12,设 CD=x,则 BC=12 - x。
此时 AC=$\sqrt{BC^2 + AB^2}=\sqrt{(12 - x)^2 + 2^2}=\sqrt{(12 - x)^2 + 4}$,CE=$\sqrt{CD^2 + DE^2}=\sqrt{x^2 + 3^2}=\sqrt{x^2 + 9}$,所以代数式$\sqrt{x^2 + 4}+\sqrt{(12 - x)^2 + 9}$的最小值即为 AC+CE 的最小值。
作点 A 关于 BD 的对称点 A',连接 A'E 交 BD 于点 C,A'E 的长即为最小值。
过 A'作 A'F⊥ED 延长线于 F,则 A'F=BD=12,EF=DE + A'B=3 + 2=5。
在 Rt△A'FE 中,A'E=$\sqrt{A'F^2 + EF^2}=\sqrt{12^2 + 5^2}=\sqrt{144 + 25}=\sqrt{169}=13$。
所以代数式的最小值为 13。
(1) 解:因为 BD=8,CD=x,所以 BC=BD-CD=8-x。
因为 AB⊥BD,AB=5,所以在 Rt△ABC 中,AC=$\sqrt{AB^2 + BC^2}=\sqrt{5^2+(8-x)^2}=\sqrt{(8-x)^2 + 25}$。
因为 ED⊥BD,DE=1,所以在 Rt△CDE 中,CE=$\sqrt{CD^2 + DE^2}=\sqrt{x^2 + 1^2}=\sqrt{x^2 + 1}$。
所以 AC+CE=$\sqrt{(8 - x)^2 + 25}+\sqrt{x^2 + 1}$。
(2) 解:作点 A 关于直线 BD 的对称点 A',连接 A'E 交 BD 于点 C,此时 AC+CE 的值最小,最小值为 A'E 的长。
因为点 A 与 A'关于 BD 对称,AB=5,所以 A'B=AB=5,∠A'BD=∠ABD=90°,所以 A',B,D 三点共线,且 A'D=A'B + BD=5 + 8=13?(此处错误,应为 A'在 AB 延长线上,A'B=AB=5,所以 A'到 D 的水平距离为 BD=8,垂直距离为 A'B + DE=5 + 1=6?不,重新构建:过点 A'作 A'F⊥ED 交 ED 的延长线于点 F。
则 A'F=BD=8,EF=DE + A'B=1 + 5=6。
在 Rt△A'FE 中,A'E=$\sqrt{A'F^2 + EF^2}=\sqrt{8^2 + 6^2}=\sqrt{64 + 36}=\sqrt{100}=10$。
所以 AC+CE 的最小值为 10。
(3) 解:构造直角梯形,使上底为 2,下底为 3,高为 12。设梯形的下底左端点为 B,右端点为 D,上底左端点为 A,右端点为 E,AB⊥BD,DE⊥BD,AB=2,DE=3,BD=12,设 CD=x,则 BC=12 - x。
此时 AC=$\sqrt{BC^2 + AB^2}=\sqrt{(12 - x)^2 + 2^2}=\sqrt{(12 - x)^2 + 4}$,CE=$\sqrt{CD^2 + DE^2}=\sqrt{x^2 + 3^2}=\sqrt{x^2 + 9}$,所以代数式$\sqrt{x^2 + 4}+\sqrt{(12 - x)^2 + 9}$的最小值即为 AC+CE 的最小值。
作点 A 关于 BD 的对称点 A',连接 A'E 交 BD 于点 C,A'E 的长即为最小值。
过 A'作 A'F⊥ED 延长线于 F,则 A'F=BD=12,EF=DE + A'B=3 + 2=5。
在 Rt△A'FE 中,A'E=$\sqrt{A'F^2 + EF^2}=\sqrt{12^2 + 5^2}=\sqrt{144 + 25}=\sqrt{169}=13$。
所以代数式的最小值为 13。
查看更多完整答案,请扫码查看


