第103页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
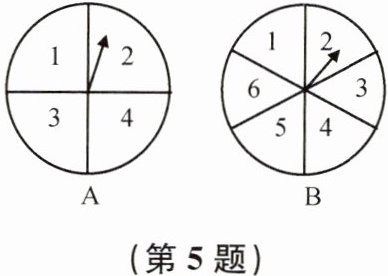
5. 如图,转盘A被均匀地分成4等份,转盘B被均匀地分成6等份,分别标上数字.同时转动转盘A与B,当转盘停止时,将指针指向的两个数字相乘.选择合适的方法求下列事件发生的概率:
(1)积为15;
(2)积为偶数.
(1)积为15;
(2)积为偶数.

答案:
【解析】:
本题考查概率的计算,需要先确定所有可能的结果,再分别计算两个事件的概率。
对于转盘$A$,指针可能指向$1$,$2$,$3$,$4$;对于转盘$B$,指针可能指向$1$,$2$,$3$,$4$,$5$,$6$。
那么两个转盘指针指向的数字组合总共有$4×6 = 24$种情况。
(1)积为$15$的情况:
通过列举法找出积为$15$的组合,即$3×5 = 15$,只有$1$种情况。
根据概率公式$P(A)=\frac{m}{n}$(其中$P(A)$表示事件$A$发生的概率,$m$表示事件$A$发生的结果数,$n$表示所有可能的结果数),可得积为$15$的概率$P_1=\frac{1}{24}$。
(2)积为偶数的情况:
先找出积为奇数的情况,两个数相乘为奇数,则这两个数都为奇数。
转盘$A$中奇数有$1$,$3$;转盘$B$中奇数有$1$,$3$,$5$。
积为奇数的组合有$2×3 = 6$种情况。
那么积为偶数的情况数$m_2 = 24 - 6 = 18$种。
所以积为偶数的概率$P_2=\frac{18}{24}=\frac{3}{4}$。
【答案】:
(1)$\frac{1}{24}$;
(2)$\frac{3}{4}$。
本题考查概率的计算,需要先确定所有可能的结果,再分别计算两个事件的概率。
对于转盘$A$,指针可能指向$1$,$2$,$3$,$4$;对于转盘$B$,指针可能指向$1$,$2$,$3$,$4$,$5$,$6$。
那么两个转盘指针指向的数字组合总共有$4×6 = 24$种情况。
(1)积为$15$的情况:
通过列举法找出积为$15$的组合,即$3×5 = 15$,只有$1$种情况。
根据概率公式$P(A)=\frac{m}{n}$(其中$P(A)$表示事件$A$发生的概率,$m$表示事件$A$发生的结果数,$n$表示所有可能的结果数),可得积为$15$的概率$P_1=\frac{1}{24}$。
(2)积为偶数的情况:
先找出积为奇数的情况,两个数相乘为奇数,则这两个数都为奇数。
转盘$A$中奇数有$1$,$3$;转盘$B$中奇数有$1$,$3$,$5$。
积为奇数的组合有$2×3 = 6$种情况。
那么积为偶数的情况数$m_2 = 24 - 6 = 18$种。
所以积为偶数的概率$P_2=\frac{18}{24}=\frac{3}{4}$。
【答案】:
(1)$\frac{1}{24}$;
(2)$\frac{3}{4}$。
6. 某地区人口状况相对稳定,某保险公司根据多年统计、综合分析,得到一张关于该地区人口寿命的表格,现摘录部分内容如下:
|年龄|达到该年龄的人数|在该年龄死亡的人数|
|40|80500|892|
|50|78009|951|
|60|69891|1200|
|70|45502|2119|
|80|16078|2001|
………||||
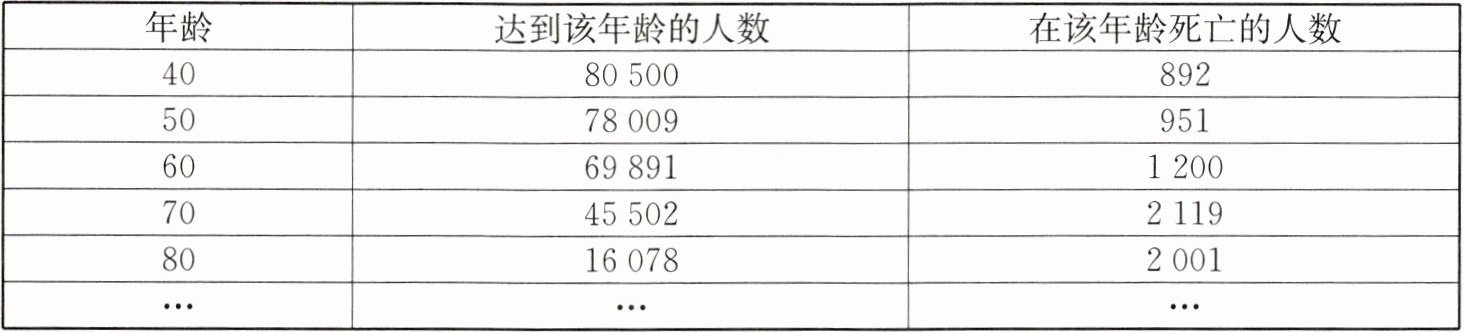
根据上表解答下列各题:
(1)该地区达到50岁的人中,不能达到51岁的概率约是多少?能达到80岁的概率约是多少?(精确到0.001)
(2)如果有20000个50岁的人购买人寿保险,当年死亡的赔偿金均为10万元,保险公司需付这一项赔偿的总额预计为多少?
|年龄|达到该年龄的人数|在该年龄死亡的人数|
|40|80500|892|
|50|78009|951|
|60|69891|1200|
|70|45502|2119|
|80|16078|2001|
………||||

根据上表解答下列各题:
(1)该地区达到50岁的人中,不能达到51岁的概率约是多少?能达到80岁的概率约是多少?(精确到0.001)
(2)如果有20000个50岁的人购买人寿保险,当年死亡的赔偿金均为10万元,保险公司需付这一项赔偿的总额预计为多少?
答案:
(1)解:不能达到51岁的概率:$P_1=\frac{951}{78009}\approx0.012$
能达到80岁的概率:$P_2=\frac{16078}{78009}\approx0.206$
(2)解:预计死亡人数:$20000×\frac{951}{78009}\approx244$(人)
赔偿总额:$244×10=2440$(万元)
答:
(1)不能达到51岁的概率约为0.012,能达到80岁的概率约为0.206;
(2)保险公司需付赔偿总额预计为2440万元。
(1)解:不能达到51岁的概率:$P_1=\frac{951}{78009}\approx0.012$
能达到80岁的概率:$P_2=\frac{16078}{78009}\approx0.206$
(2)解:预计死亡人数:$20000×\frac{951}{78009}\approx244$(人)
赔偿总额:$244×10=2440$(万元)
答:
(1)不能达到51岁的概率约为0.012,能达到80岁的概率约为0.206;
(2)保险公司需付赔偿总额预计为2440万元。
7. 某班有50位学生,每位学生都有一个序号,将50张编有学生序号(从1号到50号)的卡片(除序号不同外其他均相同)充分洗匀,从中任意抽取1张.
(1)在序号中,20倍数的有20,40,能整除20的有1,2,4,5,10(为了不重复计数,20只计一次),求取到的卡片上序号是20的倍数或能整除20的概率.
(2)若规定取到的卡片上序号是k(k是满足1≤k≤50的整数),则k的倍数或能整除k(不重复计数)的序号的学生能参加某项活动,这一规定是否公平?请说明理由.
(3)请你设计一个规定,能公平地选出10位学生参加这项活动,并说明你的规定是符合要求的.
(1)在序号中,20倍数的有20,40,能整除20的有1,2,4,5,10(为了不重复计数,20只计一次),求取到的卡片上序号是20的倍数或能整除20的概率.
(2)若规定取到的卡片上序号是k(k是满足1≤k≤50的整数),则k的倍数或能整除k(不重复计数)的序号的学生能参加某项活动,这一规定是否公平?请说明理由.
(3)请你设计一个规定,能公平地选出10位学生参加这项活动,并说明你的规定是符合要求的.
答案:
(1)解:20的倍数有20,40;能整除20的有1,2,4,5,10,20。不重复计数的序号共有1,2,4,5,10,20,40,共7个。总共有50张卡片,所以概率为7/50。
(2)解:不公平。例如,k=1时,1的倍数有50个,能整除1的有1个,不重复计数共50个;k=50时,50的倍数有1个,能整除50的有1,2,5,10,25,50,共6个。不同k对应的符合条件的序号数量不同,即每个学生被选中的概率不同,所以不公平。
(3)解:规定抽到序号末位数字为0或5的学生参加活动。1-50中末位数字为0或5的序号有5,10,15,20,25,30,35,40,45,50,共10个,每个序号被抽到的概率均为10/50=1/5,能公平选出10位学生。
(1)解:20的倍数有20,40;能整除20的有1,2,4,5,10,20。不重复计数的序号共有1,2,4,5,10,20,40,共7个。总共有50张卡片,所以概率为7/50。
(2)解:不公平。例如,k=1时,1的倍数有50个,能整除1的有1个,不重复计数共50个;k=50时,50的倍数有1个,能整除50的有1,2,5,10,25,50,共6个。不同k对应的符合条件的序号数量不同,即每个学生被选中的概率不同,所以不公平。
(3)解:规定抽到序号末位数字为0或5的学生参加活动。1-50中末位数字为0或5的序号有5,10,15,20,25,30,35,40,45,50,共10个,每个序号被抽到的概率均为10/50=1/5,能公平选出10位学生。
查看更多完整答案,请扫码查看


