第64页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
9. 用一个半径为4、面积为$24\pi$的扇形围成一个圆锥的侧面,该圆锥的底面半径为______
6
.
答案:
6
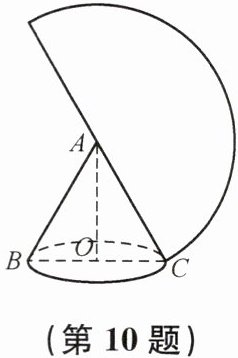
10. 如图,一个圆锥的高为$3\sqrt{3}\ cm$,侧面展开图恰好是半圆.求:(1)圆锥的母线长与底面半径之比;(2)圆锥的侧面积(结果保留$\pi$).

答案:
解:过点A作AO⊥BC于点O,易知点O为底面
圆心
设圆锥高为h,底面半径为r,母线长AC=l
∵侧面展开图是半圆
∴2πr=πl
∴l:r=2:1
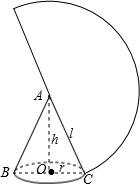
(2)解:
∵$l^2=h^2+r^2,$$h=3\sqrt{ 3}l=2r$
∴$(2r)^2=(3\sqrt{ 3})^2+r^2$
解得$r=3\ \mathrm {cm}$
∵$r=3\ \mathrm {cm},$l=2r
∴$l=6\ \mathrm {cm}$
∴圆锥侧面积为$\frac {1}{2}πl^2=18π(\ \mathrm {cm^2})$
解:过点A作AO⊥BC于点O,易知点O为底面
圆心
设圆锥高为h,底面半径为r,母线长AC=l
∵侧面展开图是半圆
∴2πr=πl
∴l:r=2:1

(2)解:
∵$l^2=h^2+r^2,$$h=3\sqrt{ 3}l=2r$
∴$(2r)^2=(3\sqrt{ 3})^2+r^2$
解得$r=3\ \mathrm {cm}$
∵$r=3\ \mathrm {cm},$l=2r
∴$l=6\ \mathrm {cm}$
∴圆锥侧面积为$\frac {1}{2}πl^2=18π(\ \mathrm {cm^2})$
11. 小明要制作一个圆锥模型,操作规则:在一张边长为16 cm的正方形纸片上剪出一个扇形和一个圆,使得扇形围成圆锥的侧面时,圆恰好是该圆锥的底面.他首先设计了如图所示的方案一,发现这种方案不可行,于是调整了扇形和圆的半径,设计了如图所示的方案二. (1)请说明方案一不可行的理由. (2)判断方案二是否可行.若可行,请确定圆锥的母线长及其底面圆半径;若不可行,请说明理由.


答案:
解:
(1) 如图, 连接 AC, E 为$ \odot O_{1} $和扇形的切点
$\because $扇 形的弧长为$ \frac{90 \times \pi \times 16}{180}=8 \pi , $圆锥底面周长为$ 2 \pi r\ $
$\therefore 2 \pi r=8 \pi , $解得 r=4 , 即$ \odot O_{1} $的半径$ O_{1} E=4 \mathrm{~cm}\ $
过 O_{1} 作$ O_{1} F \perp C D $于点 F
$\therefore \triangle C O_{1} F $为等腰直角三角 形
$\therefore O_{1} C=\sqrt{2} O_{1} F=\sqrt{2} O_{1} E=4 \sqrt{2} \mathrm{~cm}$
$\because A E= A B=16 \mathrm{~cm}$
而制作这样的圆锥实际需要正方形纸片 的对角
线长为$ A E+E O_{1}+O_{1} C=(20+4 \sqrt{2}) \mathrm{cm}\ $
$20+4 \sqrt{2}\gt 16 \sqrt{2}$
$\therefore $方案一不可行
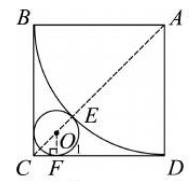
(2)解:方案二可行. 求解过程如下:
设圆锥底面圆的半径为$ r\ \mathrm {cm},$ 圆锥的母线长为
$R\ \mathrm {cm},$
$\because $在一块边长为$ 16\ \mathrm {cm} $的正方形纸片上,
$\therefore $正方形对角线长为$ 16 \sqrt{2}\ \mathrm {cm},$
则$ (1+\sqrt{2})\ \mathrm {r}+R=16 \sqrt{2},$ ①
$2 \pi r= \frac {2 \pi R}{4}. ②$
由①②可得$ R=\frac {64 \sqrt{2}}{5+\sqrt{2}}=\frac {320 \sqrt{2}-128}{23},$
$r=\frac {16 \sqrt{2}}{5+\sqrt{2}}=\frac {80 \sqrt{2}-32}{23}.$
故所求圆锥的母线长为$ \frac {320 \sqrt{2}-128}{23}\ \mathrm {cm},$
底面圆的半径为$ \frac {80 \sqrt{2}-32}{23}\ \mathrm {cm}.$
解:
(1) 如图, 连接 AC, E 为$ \odot O_{1} $和扇形的切点
$\because $扇 形的弧长为$ \frac{90 \times \pi \times 16}{180}=8 \pi , $圆锥底面周长为$ 2 \pi r\ $
$\therefore 2 \pi r=8 \pi , $解得 r=4 , 即$ \odot O_{1} $的半径$ O_{1} E=4 \mathrm{~cm}\ $
过 O_{1} 作$ O_{1} F \perp C D $于点 F
$\therefore \triangle C O_{1} F $为等腰直角三角 形
$\therefore O_{1} C=\sqrt{2} O_{1} F=\sqrt{2} O_{1} E=4 \sqrt{2} \mathrm{~cm}$
$\because A E= A B=16 \mathrm{~cm}$
而制作这样的圆锥实际需要正方形纸片 的对角
线长为$ A E+E O_{1}+O_{1} C=(20+4 \sqrt{2}) \mathrm{cm}\ $
$20+4 \sqrt{2}\gt 16 \sqrt{2}$
$\therefore $方案一不可行

(2)解:方案二可行. 求解过程如下:
设圆锥底面圆的半径为$ r\ \mathrm {cm},$ 圆锥的母线长为
$R\ \mathrm {cm},$
$\because $在一块边长为$ 16\ \mathrm {cm} $的正方形纸片上,
$\therefore $正方形对角线长为$ 16 \sqrt{2}\ \mathrm {cm},$
则$ (1+\sqrt{2})\ \mathrm {r}+R=16 \sqrt{2},$ ①
$2 \pi r= \frac {2 \pi R}{4}. ②$
由①②可得$ R=\frac {64 \sqrt{2}}{5+\sqrt{2}}=\frac {320 \sqrt{2}-128}{23},$
$r=\frac {16 \sqrt{2}}{5+\sqrt{2}}=\frac {80 \sqrt{2}-32}{23}.$
故所求圆锥的母线长为$ \frac {320 \sqrt{2}-128}{23}\ \mathrm {cm},$
底面圆的半径为$ \frac {80 \sqrt{2}-32}{23}\ \mathrm {cm}.$
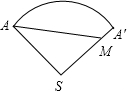
12. 如图,圆锥底面的半径为10 cm,高为$10\sqrt{15}\ cm$. (1)求圆锥的全面积;(2)若一只蚂蚁从底面上的点A出发绕圆锥一周回到SA上的点M处,且SM= 3AM,求它所走的最短距离.
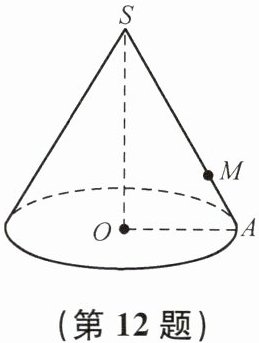

答案:
解:
(2)沿母线SA将圆锥的侧面展开,如下图
则线段AM的长就是蚂蚁所走的最短距离由
(1)知
$SA=40\ \mathrm {cm},$弧$AA'=20\pi\ \mathrm {cm}$
$\because \dfrac{n\pi \times 40}{180}=20\pi\ \mathrm {cm}$
$\therefore \angle S=n=\dfrac{180\times 20\pi }{40\pi }=90^{\circ}$
$\because SA'=SA=40\ \mathrm {cm},$SM=3A'M
$\therefore SM=30\ \mathrm {cm}$
$\therefore $在$Rt\triangle ASM$中,由勾股定理得$AM=50(\ \mathrm {cm})$
所以,蚂蚁所走的最短距离是$50\ \mathrm {cm}$
解:
(2)沿母线SA将圆锥的侧面展开,如下图
则线段AM的长就是蚂蚁所走的最短距离由
(1)知
$SA=40\ \mathrm {cm},$弧$AA'=20\pi\ \mathrm {cm}$
$\because \dfrac{n\pi \times 40}{180}=20\pi\ \mathrm {cm}$
$\therefore \angle S=n=\dfrac{180\times 20\pi }{40\pi }=90^{\circ}$
$\because SA'=SA=40\ \mathrm {cm},$SM=3A'M
$\therefore SM=30\ \mathrm {cm}$
$\therefore $在$Rt\triangle ASM$中,由勾股定理得$AM=50(\ \mathrm {cm})$
所以,蚂蚁所走的最短距离是$50\ \mathrm {cm}$

查看更多完整答案,请扫码查看


