第55页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
17. (★★)(张家界)如图23.1-12,在平面直角坐标系中,将边长为1的正方形OABC绕点O顺时针旋转$45^{\circ}后得到正方形OA_1B_1C_1$,依此方式,绕点O连续旋转2019次得到正方形$OA_{2019}B_{2019}C_{2019}$,那么点$A_{2019}$的坐标是【 】

A.$(\frac{\sqrt{2}}{2},-\frac{\sqrt{2}}{2})$
B.$(1,0)$
C.$(-\frac{\sqrt{2}}{2},-\frac{\sqrt{2}}{2})$
D.$(0,-1)$

A.$(\frac{\sqrt{2}}{2},-\frac{\sqrt{2}}{2})$
B.$(1,0)$
C.$(-\frac{\sqrt{2}}{2},-\frac{\sqrt{2}}{2})$
D.$(0,-1)$
答案:
A 提示:
∵ 四边形$OABC$是正方形,且$OA=1$,
∴ 点$A$的坐标为$(0,1)$.
∵ 将正方形$OABC$绕点$O$顺时针旋转$45°$后得到正方形$OA_1B_1C_1$,…,
∴ $A_1\left( \frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2} \right)$,$A_2(1,0)$,$A_3\left( \frac{\sqrt{2}}{2},-\frac{\sqrt{2}}{2} \right)$,…,如图9,发现是8次一循环,
∴ $2019÷8=252\cdots\cdots3$,
∴ 点$A_{2019}$的坐标为$\left( \frac{\sqrt{2}}{2},-\frac{\sqrt{2}}{2} \right)$.
∵ 四边形$OABC$是正方形,且$OA=1$,
∴ 点$A$的坐标为$(0,1)$.
∵ 将正方形$OABC$绕点$O$顺时针旋转$45°$后得到正方形$OA_1B_1C_1$,…,
∴ $A_1\left( \frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2} \right)$,$A_2(1,0)$,$A_3\left( \frac{\sqrt{2}}{2},-\frac{\sqrt{2}}{2} \right)$,…,如图9,发现是8次一循环,
∴ $2019÷8=252\cdots\cdots3$,
∴ 点$A_{2019}$的坐标为$\left( \frac{\sqrt{2}}{2},-\frac{\sqrt{2}}{2} \right)$.
18. (★★)(苏州)如图23.1-13,在$\triangle ABC$中,点E在BC边上,$AE = AB$,将线段AC绕A点旋转到AF的位置,使得$\angle CAF = \angle BAE$,连接EF,EF与AC交于点G.
(1)求证:$EF = BC$;
(2)若$\angle ABC = 65^{\circ}$,$\angle ACB = 28^{\circ}$,求$\angle FGC$的度数.
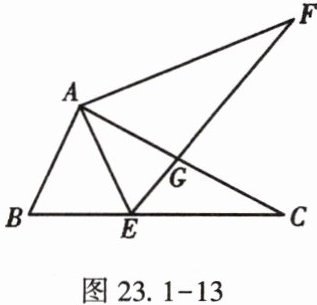
(1)求证:$EF = BC$;
(2)若$\angle ABC = 65^{\circ}$,$\angle ACB = 28^{\circ}$,求$\angle FGC$的度数.

答案:
(1)
∵ $\angle CAF=\angle BAE$,
∴ $\angle CAF+\angle CAE=\angle BAE+\angle CAE$,即$\angle BAC=\angle EAF$.
∵ 将线段$AC$绕$A$点旋转到$AF$的位置,
∴ $AC=AF$. 在$\triangle ABC$与$\triangle AEF$中,$\begin{cases} AB=AE, \\ \angle BAC=\angle EAF, \\ AC=AF, \end{cases}$
∴ $\triangle ABC\cong\triangle AEF(SAS)$,
∴ $EF=BC$.
(2)
∵ $AB=AE$,$\angle ABC=65°$,
∴ $\angle AEB=65°$,
∴ $\angle BAE=180° - 65°×2=50°$,
∴ $\angle CAF=\angle BAE=50°$.
∵ $\triangle ABC\cong\triangle AEF$,
∴ $\angle F=\angle ACB=28°$,
∴ $\angle FGC=\angle CAF+\angle F=50° + 28°=78°$.
(1)
∵ $\angle CAF=\angle BAE$,
∴ $\angle CAF+\angle CAE=\angle BAE+\angle CAE$,即$\angle BAC=\angle EAF$.
∵ 将线段$AC$绕$A$点旋转到$AF$的位置,
∴ $AC=AF$. 在$\triangle ABC$与$\triangle AEF$中,$\begin{cases} AB=AE, \\ \angle BAC=\angle EAF, \\ AC=AF, \end{cases}$
∴ $\triangle ABC\cong\triangle AEF(SAS)$,
∴ $EF=BC$.
(2)
∵ $AB=AE$,$\angle ABC=65°$,
∴ $\angle AEB=65°$,
∴ $\angle BAE=180° - 65°×2=50°$,
∴ $\angle CAF=\angle BAE=50°$.
∵ $\triangle ABC\cong\triangle AEF$,
∴ $\angle F=\angle ACB=28°$,
∴ $\angle FGC=\angle CAF+\angle F=50° + 28°=78°$.
1. (★) 把一个图形绕着某一点旋转____,如果它能够与____重合,那么就说这两个图形关于这个点对称或中心对称,这个点叫做____(简称____). 这两个图形在旋转后能重合的对应点叫做关于____的对称点.
答案:
180° 另一个图形 对称中心 中心 对称中心
2. (★) 中心对称的性质:中心对称的两个图形,对称点所连线段都经过____,而且被____所平分. 中心对称的两个图形是____.
答案:
对称中心 对称中心 全等图形
查看更多完整答案,请扫码查看


