第80页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
学校组织知识竞赛,共设20道选择题,各题分值相同,每题必答.如表记录了3名参赛者的得分情况,则参赛者F的得分可能为(
|参赛者|答对题数|答错题数|得分|
|A|20|0|100|
|C|18|2|88|
|E|10|10|40|
A.58
B.62
C.78
D.93
A
)|参赛者|答对题数|答错题数|得分|
|A|20|0|100|
|C|18|2|88|
|E|10|10|40|
A.58
B.62
C.78
D.93
答案:
A 【解析】由表可知,参赛者A答对20道题,答错0道题,共得到100分,所以答对一道题得100÷20 = 5(分).参赛者E答对10道题,得10×5 = 50(分),答错10道题,最终得分为40分,所以答错一道题得(40 - 50)÷10 = -1(分).设参赛者F答对x道题,则答错(20 - x)道题,所以参赛者F得分为5x-(20 - x)=(6x - 20)分.当6x - 20 = 58时,解得x = 13,符合题意;当6x - 20 = 62时,解得x = $\frac{41}{3}$,不符合题意;当6x - 20 = 78时,解得x = $\frac{49}{3}$,不符合题意;当6x - 20 = 93时,解得x = $\frac{113}{6}$,不符合题意.故选A.
如图,跑道由两个半圆部分和两条直跑道AD,BC组成,两个半圆跑道的长都是122m,两条直跑道的长都是85m.小斌站在C处,小强站在B处,两人同时沿逆时针方向跑步,小斌每秒跑7m,小强每秒跑12m.当小强第一次追上小斌时,他们的位置在(
A.半圆跑道AB上
B.直跑道BC上
C.半圆跑道CD上
D.直跑道AD上
C
)A.半圆跑道AB上
B.直跑道BC上
C.半圆跑道CD上
D.直跑道AD上
答案:
C 【解析】设x秒后,小强第一次追上小斌.根据题意得12x - 7x = 85,解得x = 17,所以7x = 7×17 = 119.因为119<122,所以当小强第一次追上小斌时,他们的位置在半圆跑道CD上.
3[2024安徽蚌埠期末,中]如图,甲、乙两动点分别从正方形ABCD的顶点A,C同时沿正方形的边开始匀速运动,甲按顺时针方向运动,乙按逆时针方向运动,若乙的速度是甲的3倍,那么它们第一次相遇在AD边上,则它们第2023次相遇在______边上.
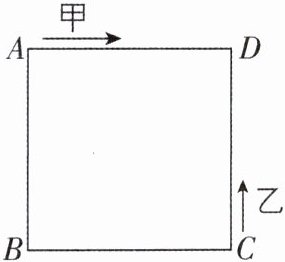

BC
答案:
BC 【解析】设正方形的边长为a.因为乙的速度是甲的速度的3倍,运动时间相同,所以甲、乙所运动的路程比为1:3.由题意知,①第一次相遇时甲、乙所运动的路程和为2a,乙所运动的路程为2a×$\frac{3}{1 + 3}=\frac{3a}{2}$,甲所运动的路程为2a×$\frac{1}{1 + 3}=\frac{a}{2}$,在AD边的中点相遇;②第一次相遇到第二次相遇时甲、乙所运动的路程和为4a,乙所运动的路程为4a×$\frac{3}{1 + 3}=3a$,甲所运动的路程为4a×$\frac{1}{1 + 3}=a$,在CD边的中点相遇;③第二次相遇到第三次相遇时甲、乙所运动的路程和为4a,乙所运动的路程为4a×$\frac{3}{1 + 3}=3a$,甲所运动的路程为4a×$\frac{1}{1 + 3}=a$,在BC边的中点相遇;④第三次相遇到第四次相遇时甲、乙所运动的路程和为4a,乙所运动的路程为4a×$\frac{3}{1 + 3}=3a$,甲所运动的路程为4a×$\frac{1}{1 + 3}=a$,在AB边的中点相遇;⑤第四次相遇到第五次相遇时甲、乙所运动的路程和为4a,乙所运动的路程为4a×$\frac{3}{1 + 3}=3a$,甲所运动的路程为4a×$\frac{1}{1 + 3}=a$,在AD边的中点相遇.综上可知,每四次一个循环.因为2023÷4 = 505……3,所以它们第2023次相遇在边BC上.故答案为BC.
4[中]在一次知识竞赛中,甲、乙两班各有50位同学参加比赛,每位同学都需要完成三道题,竞赛规则:答对一题得10分,答错扣10分.
(1)请写出每位同学所有可能的得分情况.
(2)甲班的答题情况:有2位同学全部答错,全对的人数比答对1题人数的3倍少6人,答对2题的人数是答对1题人数的2倍;乙班的答题情况:没有同学全部答错,答对1题人数的3倍和答对2题的人数之和等于全部答对的人数.
①求甲班全部答对的人数;
②请判断甲、乙两班哪个班的得分更高,并说明理由.
(1)请写出每位同学所有可能的得分情况.
(2)甲班的答题情况:有2位同学全部答错,全对的人数比答对1题人数的3倍少6人,答对2题的人数是答对1题人数的2倍;乙班的答题情况:没有同学全部答错,答对1题人数的3倍和答对2题的人数之和等于全部答对的人数.
①求甲班全部答对的人数;
②请判断甲、乙两班哪个班的得分更高,并说明理由.
答案:
【解】
(1)若答对1题,则答错2题,得分为1×10 - 2×10 = -10(分);若答对2题,则答错1题,得分为2×10 - 1×10 = 10(分);若答对3题,得分为3×10 = 30(分);若答错3题,得分为0 - 3×10 = -30(分).答:每位同学所有可能的得分情况是 -30分、 -10分、10分和30分.
(2)①设甲班答对1题的有x人.由题意得2+(3x - 6)+2x+x = 50,解得x = 9,则3×9 - 6 = 21(人).答:甲班全部答对的人数是21人.
②乙班得分更高.理由:由①得,甲班答对3题的有21人,答对2题的有18人,答对1题的有9人,全部答错的有2人,故甲班的得分为21×30+18×10 - 9×10 - 2×30 = 660(分).设乙班全部答对的有a人,答对1题的有b人,则答对2题的有(a - 3b)人,所以a+b+(a - 3b)=50,即a - b = 25,故乙班得分为30a+10(a - 3b)-10b = 40(a - b)=1000(分).因为1000>660,所以乙班得分更高.
(1)若答对1题,则答错2题,得分为1×10 - 2×10 = -10(分);若答对2题,则答错1题,得分为2×10 - 1×10 = 10(分);若答对3题,得分为3×10 = 30(分);若答错3题,得分为0 - 3×10 = -30(分).答:每位同学所有可能的得分情况是 -30分、 -10分、10分和30分.
(2)①设甲班答对1题的有x人.由题意得2+(3x - 6)+2x+x = 50,解得x = 9,则3×9 - 6 = 21(人).答:甲班全部答对的人数是21人.
②乙班得分更高.理由:由①得,甲班答对3题的有21人,答对2题的有18人,答对1题的有9人,全部答错的有2人,故甲班的得分为21×30+18×10 - 9×10 - 2×30 = 660(分).设乙班全部答对的有a人,答对1题的有b人,则答对2题的有(a - 3b)人,所以a+b+(a - 3b)=50,即a - b = 25,故乙班得分为30a+10(a - 3b)-10b = 40(a - b)=1000(分).因为1000>660,所以乙班得分更高.
(1)A,B两点间的距离为
(2)甲、乙在数轴上的哪个数对应的点相遇?
(3)多少秒时,甲、乙相距10个单位长度?
(4)若乙到达A点后立刻掉头并保持速度不变向右运动,则甲到达B点前,甲、乙还能在数轴上相遇吗? 若能,求出相遇点所对应的数;若不能,请说明理由.
60
个单位长度;乙到达A点时共运动了15
秒.(2)甲、乙在数轴上的哪个数对应的点相遇?
【解】设甲、乙经过x秒相遇.根据题意得x+4x = 60,解得x = 12,所以 - 40+x = - 28.答:甲、乙在数轴上 - 28对应的点相遇.
(3)多少秒时,甲、乙相距10个单位长度?
【解】设y秒时,甲、乙相距10个单位长度.相遇前,根据题意得,y+4y = 60 - 10,解得y = 10;相遇后,根据题意得y+4y - 60 = 10,解得y = 14.答:10秒或14秒时,甲、乙相距10个单位长度.
(4)若乙到达A点后立刻掉头并保持速度不变向右运动,则甲到达B点前,甲、乙还能在数轴上相遇吗? 若能,求出相遇点所对应的数;若不能,请说明理由.
【解】能.乙到达A点时,甲位于 - 40+15 = - 25对应的点上,乙追上甲需要15÷(4 - 1)=5(秒),则相遇点对应的数是 - 25+5 = - 20.
答案:
【解】
(1)A,B两点间的距离为|-40 - 20| = 60(个)单位长度,乙到达A点时共运动了60÷4 = 15(秒).故答案为60,15.
(2)设甲、乙经过x秒相遇.根据题意得x+4x = 60,解得x = 12,所以 - 40+x = - 28.答:甲、乙在数轴上 - 28对应的点相遇.
(3)设y秒时,甲、乙相距10个单位长度.相遇前,根据题意得,y+4y = 60 - 10,解得y = 10;相遇后,根据题意得y+4y - 60 = 10,解得y = 14.答:10秒或14秒时,甲、乙相距10个单位长度.
(4)能.乙到达A点时,甲位于 - 40+15 = - 25对应的点上,乙追上甲需要15÷(4 - 1)=5(秒),则相遇点对应的数是 - 25+5 = - 20.
(1)A,B两点间的距离为|-40 - 20| = 60(个)单位长度,乙到达A点时共运动了60÷4 = 15(秒).故答案为60,15.
(2)设甲、乙经过x秒相遇.根据题意得x+4x = 60,解得x = 12,所以 - 40+x = - 28.答:甲、乙在数轴上 - 28对应的点相遇.
(3)设y秒时,甲、乙相距10个单位长度.相遇前,根据题意得,y+4y = 60 - 10,解得y = 10;相遇后,根据题意得y+4y - 60 = 10,解得y = 14.答:10秒或14秒时,甲、乙相距10个单位长度.
(4)能.乙到达A点时,甲位于 - 40+15 = - 25对应的点上,乙追上甲需要15÷(4 - 1)=5(秒),则相遇点对应的数是 - 25+5 = - 20.
查看更多完整答案,请扫码查看


