《2025年初中必刷题七年级数学上册人教版》

1 [2024四川内江中考]下列单项式中,$ab^{3}$的同类项是( A )

A.$3ab^{3}$
B.$2a^{2}b^{3}$
C.$-a^{2}b^{2}$
D.$a^{3}b$

答案： A 【解析】根据同类项的定义可知,$ab^{3}$的同类项是$3ab^{3}$.故选A.

2 [2024吉林长春中考]单项式$-2a^{2}b$的次数为3.

答案： 3 【解析】因为单项式中所有字母的指数和叫作这个单项式的次数,所以单项式$-2a^{2}b$的次数是$2+1=3$.故答案为3.

3 [2024四川绵阳中考]已知单项式$3a^{2}b与-2a^{2}b^{n-1}$是同类项,则$n= $2.

答案： 2 【解析】由同类项的定义可知$n-1=1$,解得$n=2$.

4 [2024贵州中考]计算$2a+3a$的结果正确的是(A)
A.$5a$
B.$6a$
C.$5a^{2}$
D.$6a^{2}$

答案： A 【解析】$2a+3a=5a$,故选A.

5 [2024江苏常州中考]计算$2a^{2}-a^{2}$的结果是(B)
A.2
B.$a^{2}$
C.$3a^{2}$
D.$2a^{4}$

答案： B 【解析】$2a^{2}-a^{2}=a^{2}$,故选B.

6 [2024四川德阳中考]若一个多项式加上$y^{2}+3xy-4$,结果是$3xy+2y^{2}-5$,则这个多项式为$y^{2}-1$.

答案： $y^{2}-1$ 【解析】$3xy+2y^{2}-5-(y^{2}+3xy-4)=3xy+2y^{2}-5-y^{2}-3xy+4=y^{2}-1$.故答案为$y^{2}-1$.

7 [贵州六盘水中考]已知$(x+y)^{4}= a_{1}x^{4}+a_{2}x^{3}y+a_{3}x^{2}y^{2}+a_{4}xy^{3}+a_{5}y^{4}$,则$a_{1}+a_{2}+a_{3}+a_{4}+a_{5}$的值是(C)
A.4
B.8
C.16
D.32

答案： C 【解析】在$(x+y)^{4}=a_{1}x^{4}+a_{2}x^{3}y+a_{3}x^{2}y^{2}+a_{4}xy^{3}+a_{5}y^{4}$中,令$x=y=1$,得$2^{4}=a_{1}+a_{2}+a_{3}+a_{4}+a_{5}$,所以$a_{1}+a_{2}+a_{3}+a_{4}+a_{5}=16$.故选C.

8 [2023辽宁沈阳中考]当$a+b= 3$时,代数式$2(a+2b)-(3a+5b)+5$的值为2.

答案： 2 【解析】$2(a+2b)-(3a+5b)+5=2a+4b-3a-5b+5=-a-b+5=-(a+b)+5$.当$a+b=3$时,原式$=-3+5=2$,故答案为2.

在“点燃我的梦想,数学皆有可能”数学创新设计活动中,“智多星”小强设计了一个数学探究活动:对依次排列的两个整式$m$,$n$按如下规律进行操作:
第1次操作后得到整式串$m$,$n$,$n-m$;
第2次操作后得到整式串$m$,$n$,$n-m$,$-m$;
第3次操作后……
其操作规则为每次操作增加的项,都是用上一次操作得到的最末项减去其前一项的差,小强将这个活动命名为“回头差”游戏.
则该“回头差”游戏第2023次操作后得到的整式串各项之和是(D)
A.$m+n$
B.$m$
C.$n-m$
D.$2n$

答案： D 【解析】第1次操作后得到整式串$m$,$n$,$n-m$;第2次操作后得到整式串$m$,$n$,$n-m$,$-m$;第3次操作后得到整式串$m$,$n$,$n-m$,$-m$,$-n$;第4次操作后得到整式串$m$,$n$,$n-m$,$-m$,$-n$,$-n+m$;第5次操作后得到整式串$m$,$n$,$n-m$,$-m$,$-n$,$-n+m$,$m$;第6次操作后得到整式串$m$,$n$,$n-m$,$-m$,$-n$,$-n+m$,$m$,$n$;第7次操作后得到整式串$m$,$n$,$n-m$,$-m$,$-n$,$-n+m$,$m$,$n$,$n-m$;…归纳可得,整式串中每6个整式为一循环.则第2023次操作后得到整式串$m$,$n$,$n-m$,$-m$,$-n$,$-n+m$,…,$m$,$n$,$n-m$,共2025个整式.每6个整式的整式之和为$m+n+(n-m)+(-m)+(-n)+(-n+m)=0$.因为$2025÷6=337\cdots\cdots3$,所以第2023次操作后得到的整式串各项之和即为最后三项之和,为$m+n+(n-m)=2n$.故选D.

在日历上,某些数满足一定的规律.如图是某年8月份的日历,任意选择其中所示的含4个数字的方框部分,设右上角的数字为$a$,则下列叙述中正确的是(D)
A.左上角的数字为$a+1$
B.左下角的数字为$a+7$
C.右下角的数字为$a+8$
D.方框中4个位置的数相加,结果是4的倍数

答案： D 【解析】日历中的数字规律:同一行中后面的数字比它前面的与其相邻的数字大1,同一列中下一行的数字比上一行的大7.任意选择如题图所示的含4个数字的方框部分,若设右上角的数字为$a$,则左上角的数字为$a-1$,故选项A错误,不符合题意;左下角的数字为$a+6$,故选项B错误,不符合题意;右下角的数字为$a+7$,故选项C错误,不符合题意;把方框中4个位置的数字相加,即$a-1+a+a+6+a+7=4a+12=4(a+3)$,结果是4的倍数,故选项D正确.故选D.

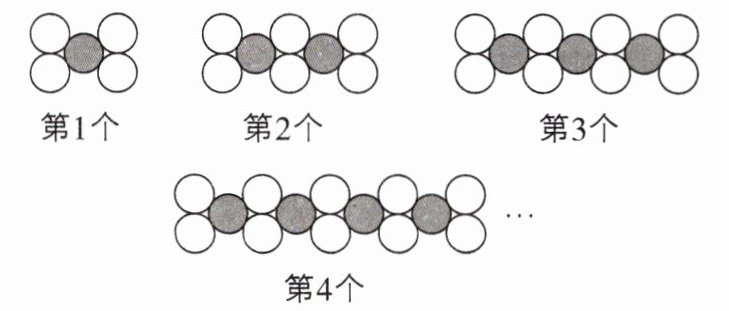
11 [2023山西中考]如图是一组有规律的图案,它由若干个大小相同的圆片组成.第1个图案中有4个白色圆片,第2个图案中有6个白色圆片,第3个图案中有8个白色圆片,第4个图案中有10个白色圆片,…,依此规律,第$n$个图案中有$(2+2n)$个白色圆片(用含$n$的代数式表示).

答案： $(2+2n)$ 【解析】第1个图案中有4个白色圆片,第2个图案中有$4+2=6$(个)白色圆片,第3个图案中有$4+2×2=8$(个)白色圆片,第4个图案中有$4+2×3=10$(个)白色圆片,…,所以第$n$个图案中有$4+2(n-1)=(2+2n)$个白色圆片.故答案为$(2+2n)$.