第12页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
一、选择题(每小题 5 分,共 30 分)
1 下列各数中,负分数有(
$-2\frac {4}{7},|-1.5|,0,-3.14,-\frac {1}{2022},200,-51,-|-0.5|$。
A.1 个
B.2 个
C.3 个
D.4 个
1 下列各数中,负分数有(
D
)$-2\frac {4}{7},|-1.5|,0,-3.14,-\frac {1}{2022},200,-51,-|-0.5|$。
A.1 个
B.2 个
C.3 个
D.4 个
答案:
D 【解析】负分数有$-2\frac {4}{7},-3.14,-\frac {1}{2022},$$-|-0.5|$,共4个. 故选 D.
2 [2024 湖北襄阳期中]将某蓄水池的标准水位记为 0 m,如果用正数表示水面高于标准水位的高度,那么-0.2 m 表示(
A.水面低于标准水位-0.2 m
B.水面低于标准水位 0.2 m
C.水面高于标准水位 0.2 m
D.水面水深为 0.2 m
B
)A.水面低于标准水位-0.2 m
B.水面低于标准水位 0.2 m
C.水面高于标准水位 0.2 m
D.水面水深为 0.2 m
答案:
B 【解析】因为正数表示水面高于标准水位的高度,所以-0.2 m 表示水面低于标准水位0.2 m. 故选 B.
3 [2025 贵州遵义一模]若有理数 a,b 在数轴上的对应点的位置如图所示,则下列大小关系正确的是(

A.$|b| > a$
B.$b > -a$
C.$a > -b$
D.$|a| > |b|$
A
)
A.$|b| > a$
B.$b > -a$
C.$a > -b$
D.$|a| > |b|$
答案:
A 【解析】在数轴上标出$-a,|a|,-b$和$|b|$的对应点的位置,根据数轴上左边的数小于右边的数,可得$|b|>a,b<-a,a<-b$,$|a|<|b|$. 故选 A.
4 [2025 浙江杭州西湖区校级期中]$|a| + |b| = |a + b|$,则 a,b 满足的关系是(
A.a,b 的绝对值相等
B.a,b 异号
C.$a + b$的和是非负数
D.a,b 同号或其中至少有一个为 0
D
)A.a,b 的绝对值相等
B.a,b 异号
C.$a + b$的和是非负数
D.a,b 同号或其中至少有一个为 0
答案:
D 【解析】因为$|a|+|b|=|a+b|$,所以 a,b 满足的关系是 a,b 同号或 a,b 中有一个为0 或a,b 同时为0,故选 D.
5 [2024 辽宁葫芦岛调研]如图所示,圆的周长为 4 个单位长度,在圆周的 4 等分点处分别标上字母 A,B,C,D,先将圆周上的字母 A 对应的点与数轴上的原点重合,再将圆沿着数轴向右滚动,那么圆周上与数轴上表示 1949 的点重合的点是( )

A.A
B.B
C.C
D.D

A.A
B.B
C.C
D.D
答案:
D 【解析】
识图解题 数轴上的规律问题
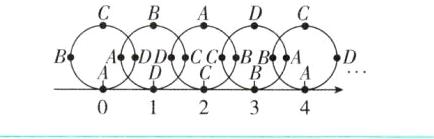
由图可以看出,以 D,C,B,A 四个字母为一次循环. 因为$1949÷4=487... 1$,所以数轴上表示 1949 的点与圆周上的字母 D 重合. 故选 D.
D 【解析】
识图解题 数轴上的规律问题

由图可以看出,以 D,C,B,A 四个字母为一次循环. 因为$1949÷4=487... 1$,所以数轴上表示 1949 的点与圆周上的字母 D 重合. 故选 D.
6 [2024 陕西西安质检]设非零有理数 a,b,c 满足$a < b < c$,且 a,c 异号,$|c| < |b| < |a|$,则$|x - a| + |x - b| + |x - (-c)|$的最小值是(
A.$\frac {|a + b + c|}{3}$
B.$|b|$
C.$c - a$
D.$-c - a$
D
)A.$\frac {|a + b + c|}{3}$
B.$|b|$
C.$c - a$
D.$-c - a$
答案:
D 【解析】因为 a,c 异号,$a<b<c$,所以$a<0$,$c>0$. 又因为$|c|<|b|<|a|$,所以$a<b<-c<0<c$.因为$|x-a|+|x-b|+|x-(-c)|$表示在数轴上数 x 对应的点到 a,b,-c 三个数对应的点的距离之和,而当$x=b$时,其距离之和最小,即$|x-a|+|x-b|+|x-(-c)|$最小,所以最小值是a 与-c 在数轴上对应的点之间的距离,即$-c - a$. 故选 D.
二、填空题(每小题 5 分,共 15 分)
7 [2024 安徽亳州期中]一种零件的长度在图纸上是$(10_{-0.02}^{+0.03})$毫米,表示这种零件的标准尺寸是
7 [2024 安徽亳州期中]一种零件的长度在图纸上是$(10_{-0.02}^{+0.03})$毫米,表示这种零件的标准尺寸是
10
毫米,加工要求最大不超过10.03
毫米,最小不小于9.98
毫米。
答案:
10 10.03 9.98 【解析】表示这种零件的标准尺寸是 10 毫米,加工要求最大不超过10.03 毫米,最小不小于9.98 毫米. 故答案为10,10.03,9.98.
8 [2025 甘肃兰州期末]比较大小:-3
<
$-(-|-2|)$。(填“>”“<”或“=”)
答案:
< 【解析】因为$-(-|-2|)=2,-3<2$,所以$-3<-(-|-2|)$. 故答案为<.
数轴上有三个点 A,B,C,且 A,B 两点间的距离是 4,B,C 两点间的距离是 2。若点 A 表示的数是-2,则点 C 表示的数是
0 或 4 或-4 或-8
。
答案:
0 或 4 或-4 或-8 【解析】在数轴上两点之间的距离等于两点所表示的数的差的绝对值. 根据 A,B 两点间的距离为4 以及点 A 表示的数为-2 可得点 B 所表示的数为 2 或-6.当点 B 表示的数为 2 时,点 C 所表示的数为0或 4. 当点 B 表示的数为-6 时,点 C 所表示的数为-8 或-4. 综上所述,点 C 表示的数为0或 4 或-4 或-8.
易错警示
已知数轴上两点之间的距离和其中一点表示的数,求另一点所表示的数时,一定要注意分类讨论,不要漏解.
思路分析
利用已知条件得到$a<b<-c<0<c$,再利用绝对值的几何意义和数形结合的思想解答即可.
易错警示
已知数轴上两点之间的距离和其中一点表示的数,求另一点所表示的数时,一定要注意分类讨论,不要漏解.
思路分析
利用已知条件得到$a<b<-c<0<c$,再利用绝对值的几何意义和数形结合的思想解答即可.
三、解答题(共 55 分)
10 [2025 四川南充质检]将下列各数填入适当的括号内:
$5,-3,\frac {3}{4},8.9,19,-\frac {6}{7},-3.14,-9,0,2\frac {3}{5}$。
分数集合:…{
整数集合:…{
非正整数集合:…{
非负数集合:…{
10 [2025 四川南充质检]将下列各数填入适当的括号内:
$5,-3,\frac {3}{4},8.9,19,-\frac {6}{7},-3.14,-9,0,2\frac {3}{5}$。
分数集合:…{
$\frac {3}{4},8.9,-\frac {6}{7},-3.14,2\frac {3}{5}$
};整数集合:…{
$5,-3,19,-9,0$
};非正整数集合:…{
$-3,-9,0$
};非负数集合:…{
$5,\frac {3}{4},8.9,19,0,2\frac {3}{5}$
}。
答案:
【解】分数集合:$\{ \frac {3}{4},8.9,-\frac {6}{7},-3.14,2\frac {3}{5},... \} ;$整数集合:$\{ 5,-3,19,-9,0,... \} ;$非正整数集合:$\{ -3,-9,0,... \} ;$非负数集合:$\{ 5,\frac {3}{4},8.9,19,0,2\frac {3}{5},... \} .$
11 已知 a,b 满足$|a| < |b| ≤ 4$,且 a,b 为整数。
(1)写出 a,b 的最大值;
(2)当 a,b 为何值时,$|a| + b$有最小值?

(1)写出 a,b 的最大值;
(2)当 a,b 为何值时,$|a| + b$有最小值?

答案:
【解】
(1)因为$|a|<|b| ≤ 4$,且 a,b 为整数,所以 a 的最大值为 3,b 的最大值为 4.
(2)因为$|a|≥0$,所以当$a=0$时,$|a|$最小.因为$|b|≤4$,所以 b 的最小值为-4. 所以当$a=0,b=-4$时,$|a| + b$有最小值.
(1)因为$|a|<|b| ≤ 4$,且 a,b 为整数,所以 a 的最大值为 3,b 的最大值为 4.
(2)因为$|a|≥0$,所以当$a=0$时,$|a|$最小.因为$|b|≤4$,所以 b 的最小值为-4. 所以当$a=0,b=-4$时,$|a| + b$有最小值.
查看更多完整答案,请扫码查看


