第43页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
甲、乙是两个成反比例关系的量,当甲减少20%时,乙 (
A.增加20%
B.减少20%
C.增加25%
D.减少25%
C
)A.增加20%
B.减少20%
C.增加25%
D.减少25%
答案:
C 【解析】因为甲和乙是两个成反比例关系的量,所以它们的乘积一定. 根据题意可得甲减少到原来的$1 - 20\%=\frac{4}{5}$,则乙需增加到原来的$1÷\frac{4}{5}=\frac{5}{4}$,所以乙增加$(5 - 4)÷4 = 25\%$,故选 C.
下面各图中,能表示正比例关系的是 (
A.销售量(个)与剩余量(个)关系图
B.工作总量(个)与人数关系图
C.销售量(件)与单价(元/件)关系图
D.距离(米)与时间(秒)关系图
B
)A.销售量(个)与剩余量(个)关系图
B.工作总量(个)与人数关系图
C.销售量(件)与单价(元/件)关系图
D.距离(米)与时间(秒)关系图
答案:
B 【解析】A 选项,销售量大约为 60 个时,剩余量为 20 个,销售量大约为 40 个时,剩余量为 40 个,$60 + 20=40 + 40 = 80$(个),可知销售量+剩余量=产品总量(一定),和一定,故销售量和剩余量不成比例关系. B 选项,人数大约为 20 人时,工作总量为 20 个,人数大约为40 人时,工作总量为 40 个,$20÷20 = 40÷40 = 1$(个/人),可知工作总量÷人数=每人加工的个数(一定),商一定,故工作总量和人数成正比例关系. C 选项,销售量为 40 件时,单价大约为 20 元/件,销售量为 20 件时,单价大约为40 元/件,则$\frac{40}{20}\neq\frac{20}{40}$,可知销售量和单价不成正比例关系. D 选项,30 秒后,时间在增加,距离不变,故距离和时间不成比例关系. 故选 B.
(1)请你完成表格.
|右边刻度数|1|2|3|4|
|砝码数|
|乘积|
(2)在本次实验中,右边刻度数和砝码数成什么比例关系?为什么?
|右边刻度数|1|2|3|4|
|砝码数|
12
|6|4
|3||乘积|
12
|12
|12
|12
|(2)在本次实验中,右边刻度数和砝码数成什么比例关系?为什么?
反比例关系.理由:因为右边刻度数和砝码数的乘积为定值,所以右边刻度数和砝码数成反比例关系.
答案:
【解】
(1)$1×12 = 2×6 = 3×4 = 4×3 = 12$. 故答案为 12,4,12,12,12,12(从左到右,从上到下).
(2)反比例关系.理由:因为右边刻度数和砝码数的乘积为定值,所以右边刻度数和砝码数成反比例关系.
(1)$1×12 = 2×6 = 3×4 = 4×3 = 12$. 故答案为 12,4,12,12,12,12(从左到右,从上到下).
(2)反比例关系.理由:因为右边刻度数和砝码数的乘积为定值,所以右边刻度数和砝码数成反比例关系.
4[2024四川成都质检,中]文具店有一种彩带,销售的数量与总价的关系如下表.
|数量/m|1|2|3|4|5|6|7|8|…|
|总价/元|3.5|7|10.5|14|17.5|21|24.5|28|…|
表中的数据还可以用下图表示.
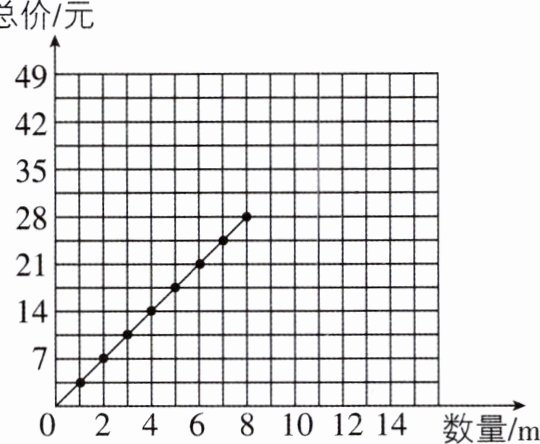
根据图象回答下面的问题.
(1)把数对$ (10, 35) 和 (12, 42) $所在的点描出来,并和上面的图象连起来再延长,你能发现什么?
(2)不计算,根据图象判断,如果买9m彩带,总价是多少?49元能买多少米彩带?
(3)小明买的彩带的米数是小丽的2倍,他花的钱是小丽的几倍?你能举出生活中成正比例关系的例子吗?

|数量/m|1|2|3|4|5|6|7|8|…|
|总价/元|3.5|7|10.5|14|17.5|21|24.5|28|…|
表中的数据还可以用下图表示.

根据图象回答下面的问题.
(1)把数对$ (10, 35) 和 (12, 42) $所在的点描出来,并和上面的图象连起来再延长,你能发现什么?
(2)不计算,根据图象判断,如果买9m彩带,总价是多少?49元能买多少米彩带?
(3)小明买的彩带的米数是小丽的2倍,他花的钱是小丽的几倍?你能举出生活中成正比例关系的例子吗?

答案:
【解】
(1)如图所示: 发现:从图中可以发现$(10,35)$和$(12,42)$对应的点也在这条直线上.
发现:从图中可以发现$(10,35)$和$(12,42)$对应的点也在这条直线上.
(2)观察上图,可知图象经过数对$(9,31.5)$和$(14,49)$所在的点,所以买 9 m 彩带,总价是31.5 元,49 元能买 14 m 彩带.
(3)他花的钱是小丽的 2 倍.如:工作效率一定,工作总量和工作时间成正比例关系(答案不唯一).
【解】
(1)如图所示:
 发现:从图中可以发现$(10,35)$和$(12,42)$对应的点也在这条直线上.
发现:从图中可以发现$(10,35)$和$(12,42)$对应的点也在这条直线上.(2)观察上图,可知图象经过数对$(9,31.5)$和$(14,49)$所在的点,所以买 9 m 彩带,总价是31.5 元,49 元能买 14 m 彩带.
(3)他花的钱是小丽的 2 倍.如:工作效率一定,工作总量和工作时间成正比例关系(答案不唯一).
查看更多完整答案,请扫码查看


