《2025年初中必刷题七年级数学上册人教版》

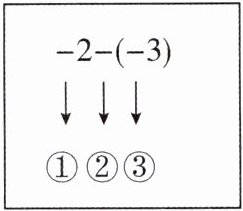
1 新考法 [2025 吉林四平期末]如图,在应用有理数减法法则计算$-2-(-3)$时,需要把“-”变成“+”的是(B)

A.①③
B.②③
C.①②
D.①②③

答案： B 【解析】$-2-(-3)=-2+(+3)$. 故选 B.

2 [2025 河北张家口调研]下列计算错误的是(B)
A.$(-9)-6= -15$
B.$(-9)-(-6)= 3$
C.$9-(-6)= 15$
D.$9-(+6)= 3$

答案： B 【解析】
A $(-9)-6=-15$ 正确
B $(-9)-(-6)=-9+6=-3$ 错误
C $9-(-6)=9+6=15$ 正确
D $9-(+6)=9-6=3$ 正确

3 如果$|n+2|+|m-7|= 0$,那么$n-m$等于(B)
A.9
B.-9
C.5
D.-5

答案： B 【解析】因为$|n+2|+|m-7|=0$,所以$n=-2$,$m=7$,所以$n-m=-2-7=-9$. 故选 B.

4 若$a的相反数是-3$,$b$的绝对值是 4,则$a-b= $7 或$-1$。

答案： 7 或$-1$ 【解析】因为$a$的相反数是$-3$,所以$a=3$. 因为$b$的绝对值是4,所以$b=\pm 4$. 当$a=3$,$b=4$时,$a-b=3-4=-1$;当$a=3$,$b=-4$时,$a-b=3-(-4)=7$. 故答案为7或$-1$.

(1)-3 和 4 关于 1 的“相对距离”为7。
(2)若$a$和 5 关于 2 的“相对距离”为 6,求$a$的值。
由题意得$|a-2|+|5-2|=6$,所以$|a-2|+3=6$,所以$|a-2|=3$,$a-2=\pm 3$,所以$a=5$或$-1$。

答案：
(1)$|-3-1|+|4-1|=4+3=7$. 故答案为7.
(2)由题意得$|a-2|+|5-2|=6$,所以$|a-2|+3=6$,所以$|a-2|=3$,$a-2=\pm 3$,所以$a=5$或$-1$.

徐志摩的《泰山日出》一文描写了“泰山佛光”的壮丽景象,已知 1 月份的泰山山脚平均气温为零下 3 摄氏度,山顶平均气温为零下 9 摄氏度,则山脚平均气温与山顶平均气温的温差是(D)
A.-6 摄氏度
B.-12 摄氏度
C.12 摄氏度
D.6 摄氏度

答案： D 【解析】由题意得$-3-(-9)=-3+9=6$(摄氏度),所以山脚平均气温与山顶平均气温的温差是6摄氏度,所以 D 选项符合题意,故选 D.

7 李明在计算$-6-a$时,误将“-a”看成了“+a”,求得结果为 3,则$-6-a= $$-15$。

答案： $-15$ 【解析】由题意得$-6+a=3$,解得$a=9$,所以$-6-a=-6-9=-15$.

8 计算：$1-(+2)+3-(+4)+5-(+6)+...-(+2022)=$$-1011$。

答案： $-1011$ 【解析】原式$=[1-(+2)]+[3-(+4)]+[5-(+6)]+\cdots +[2021-(+2022)]=-1-1-1-\cdots -1=-1011$. 故答案为$-1011$.

9 在计算“$10-3\frac {1}{2}-\frac {1}{2}$”时,甲同学的做法如下：
(1)在上面的计算过程中,开始出错的步骤是②(写出错误所在行的序号)。这一步依据的运算法则应当是同号两数相加,取与加数相同的符号,并把绝对值相加。
(2)请写出正确的计算过程。
原式$=10+(-3\frac {1}{2})+(-\frac {1}{2})=10-(3\frac {1}{2}+\frac {1}{2})=10-4=6.$

答案：
(1)在甲同学的计算过程中,开始出错的步骤是②,这一步依据的运算法则应当是同号两数相加,取与加数相同的符号,并把绝对值相加. 故答案为②;取与加数相同的符号,并把绝对值相加.
关键点拨 发现从99开始,在连续四个整数之间添加“+”和“-”可使其运算结果为0是解题的关键.
易错警示 进行有理数的减法运算时,不要混淆运算符号与性质符号,防止错解.
（2）原式$=10+(-3\frac {1}{2})+(-\frac {1}{2})=10-(3\frac {1}{2}+\frac {1}{2})=10-4=6.$