《2025年初中必刷题七年级数学上册人教版》

6 [中]如图,长为$a$,宽为$b的长方形被分割成7$部分,除阴影图形$P$,$Q$外,其余$5部分为形状和大小完全相同的小长方形O$,其中小长方形$O的宽为3$.
(1)求小长方形$O$的长(用含$a$的代数式表示).
(2)小明发现阴影图形$P与阴影图形Q的周长之和与a$值无关,他的判断是否正确? 请说明理由.

答案： 【解】
(1)因为小长方形O的宽为3,所以小长方形O的长为$a-3×3=a-9$.答:小长方形O的长为$a-9$.
(2)判断正确.理由如下:由题图可得阴影图形P的长为$a-9$,宽为$b-6$,阴影图形Q的长为9,宽为$b-(a-9)=b-a+9$,阴影图形P和阴影图形Q的周长之和为$2(a-9+b-6)+2(9+b-a+9)=2a-18+2b-12+18+2b-2a+18=4b+6$,所以阴影图形P与阴影图形Q的周长之和与$a$值无关,小明的判断正确.

7 [中]已知$A= 2x^{2}+mx-y$,$B= nx^{2}-x+6y是关于x$,$y$的多项式,其中$m$,$n$为常数.
(1)若$m= 1$,$n= -2$,化简$A+B$;
(2)若$A-2B的值与x$的取值无关,求代数式$m^{2}n^{2021}$的值.

答案： 【解】
(1)当$m=1$,$n=-2$时,$A=2x^{2}+x-y$,$B=-2x^{2}-x+6y$,所以$A+B=2x^{2}+x-y+(-2x^{2}-x+6y)=2x^{2}+x-y-2x^{2}-x+6y=5y$.
(2)$A-2B=2x^{2}+mx-y-2(nx^{2}-x+6y)=(2-2n)x^{2}+(m+2)x-13y$.由题意可得$2-2n=0$,$m+2=0$,解得$m=-2$,$n=1$,所以$m^{2}n^{2021}=(-2)^{2}×1^{2021}=4×1=4$.

8 [中]有理数$a$,$b$,$c$所对应的点在数轴上的位置如图所示,化简代数式$|a-c|-|b|-|b-a|+|b+a|$.

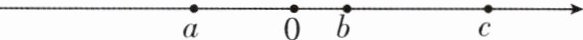
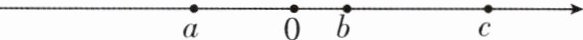
答案： 【解】由数轴可得$a-c＜0$,$b＞0$,$b-a＞0$,$a+b＜0$,所以原式$=c-a-b-b+a-b-a=-a-3b+c$.

9 [2024广东广州期中,中]已知$a$,$b$,$c$三个数在数轴上对应点的位置如图所示.
(1)在数轴上标出$-a$,$-b$,$-c$这三个数所对应的点,并将$a$,$b$,$c$,$-a$,$-b$,$-c这6$个数按从小到大的顺序用“＜”连接;
(2)化简式子$|-a-b|+|b-c|-|c-a|$;
(3)若$a+b+c= 0$,且表示数$a的点向左运动1个单位长度后在数轴上对应的数恰好与c$互为相反数,求$-3(a-b)-(c+5)-2(c+4b)$的值.

答案：
【解】
(1)在数轴上标出$-a$,$-b$,$-c$这三个数所对应的点,如下图.将$a$,$b$,$c$,$-a$,$-b$,$-c$这6个数按从小到大的顺序用“＜”连接如下:$-c＜a＜b＜-b＜-a＜c$.

(2)由题意得$a＜b＜0＜c$,所以$-a＞0$,$-b＞0$,$-c＜0$,所以$-a-b＞0$,$b-c＜0$,$c-a＞0$,所以$|-a-b|+|b-c|-|c-a|=-a-b+(c-b)-(c-a)=-a-b+c-b-c+a=-2b$.
(3)因为表示数$a$的点向左运动1个单位长度后在数轴上对应的数恰好与$c$互为相反数,所以$a-1+c=0$,所以$a+c=1$.因为$a+b+c=0$,所以$b=-1$.$-3(a-b)-(c+5)-2(c+4b)=-3a+3b-c-5-2c-8b=-3a-5b-3c-5=-3(a+c)-5b-5=-3×1-5×(-1)-5=-3+5-5=-3$.