《2025年初中必刷题七年级数学上册人教版》

1 [2024 广东东莞期中]如图所示,已知数轴上两数 $ a $ 和 $ b $,下列关系正确的是(A)

A.$ a ＜ - b ＜ b ＜ - a $
B.$ - a ＜ - b ＜ a ＜ b $
C.$ - b ＜ - a ＜ a ＜ b $
D.$ a ＜ b ＜ - b ＜ - a $

答案： A 【解析】由题图可知a＜0＜b,-a＞b,a＜-b,所以a＜-b＜b＜-a.故选A.

如图,数轴上 $ A $ 点表示的数是 $ a $,写出一个比 $ a $ 大的负分数：$-\frac{1}{2}$（答案不唯一）.

答案： $-\frac{1}{2}$（答案不唯一）【解析】由题意可知-4＜a＜-3,所以比a大的负分数可以是$-\frac{1}{2}$.故答案为$-\frac{1}{2}$(答案不唯一).

3 [2025 上海浦东新区期中]在如图所示的数轴上表示下列各数,并用“＜”把这些数连接起来.
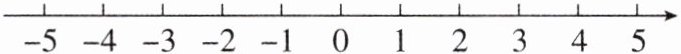
$ - 3 $,$ 3.5 $,$ - ( - 2 \frac { 1 } { 2 } ) $,$ - | - 1 | $.

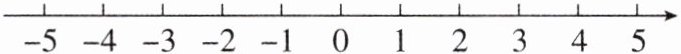
答案：
【解】$-(-2\frac{1}{2})=2\frac{1}{2}$,$-|-1|=-1$.把各数表示在数轴上,如图所示:

用“＜”连接为$-3＜-|-1|＜-(-2\frac{1}{2})＜3.5$.

4 [2025 黑龙江佳木斯期末]如果甲数的绝对值比乙数的绝对值大,那么(D)
A.甲数一定大于乙数
B.乙数一定大于甲数
C.这两个数不可能都大于 0
D.无法判断

答案： D 【解析】当甲数为-5,乙数为3时,|-5|=5,|3|=3,满足甲数的绝对值比乙数的绝对值大,但-5＜3,即甲数小于乙数,所以A选项错误,不符合题意;当甲数为5,乙数为3时,|5|=5,|3|=3,满足甲数的绝对值比乙数的绝对值大,但5＞3＞0,即甲数大于乙数,且这两个数都大于0,所以B、C选项错误,不符合题意;仅知道甲数的绝对值比乙数的绝对值大,不知道两数的正负,所以无法判断两数的大小关系,所以D选项正确,符合题意.故选D.

5 比较大小：$ - \frac { 2 } { 3 } 和 - \frac { 3 } { 4 } $.

答案： 【解】因为$|-\frac{2}{3}|=\frac{2}{3}$,$|-\frac{3}{4}|=\frac{3}{4}$,$\frac{2}{3}＜\frac{3}{4}$,所以$-\frac{2}{3}＞-\frac{3}{4}$.

6 下列选项的四个数中,最小的数是(B)
A.$ - ( - 1 ) $
B.$ - ( + 2 ) $
C.$ | - 3 | $
D.$ 0 $

答案： B 【解析】$-(-1)=1$,$-(+2)=-2$,$|-3|=3$,所以$-(+2)＜0＜-(-1)＜|-3|$.故选B.

7 下列四个式子：①$ - 3.8 ＞ - ( + 3 \frac { 3 } { 4 } ) $；②$ - ( - \frac { 3 } { 4 } ) ＞ - ( - \frac { 3 } { 5 } ) $；③$ | - 2.5 | ＞ - 2.5 $；④$ - ( - 5 \frac { 1 } { 2 } ) ＞ | + 5 \frac { 2 } { 3 } | $. 正确的是(D)
A.③④
B.①③
C.①②
D.②③

答案： D 【解析】①$-(+3\frac{3}{4})=-3.75$,根据有理数的大小关系,得$-3.8＜-(+3\frac{3}{4})$,①不正确;②$-(-\frac{3}{4})=\frac{3}{4}$,$-(-\frac{3}{5})=\frac{3}{5}$,根据有理数的大小关系,得$\frac{3}{4}＞\frac{3}{5}$,即$-(-\frac{3}{4})＞-(-\frac{3}{5})$,②正确;③$|-2.5|=2.5$,根据有理数的大小关系,得$2.5＞-2.5$,即$|-2.5|＞-2.5$,③正确;④$-(-5\frac{1}{2})=5\frac{1}{2}=5+\frac{1}{2}=5+\frac{3}{6}$,$|+5\frac{2}{3}|=5\frac{2}{3}=5+\frac{2}{3}=5+\frac{4}{6}$,根据有理数的大小关系,得$5+\frac{3}{6}＜5+\frac{4}{6}$,即$-(-5\frac{1}{2})＜|+5\frac{2}{3}|$,④不正确.综上,正确的有②③.故选D.

8 大于$ - 2 $且不大于 $ 3 $ 的整数有5个.

答案： 5 【解析】大于-2且不大于3的整数有-1,0,1,2,3,共5个.

9 核心素养 几何直观 如图所示,数轴上的点 $ A $,$ B $,$ C $,$ D $ 表示的数分别是$ - 1.5 $,$ - 3 $,$ 2 $,$ 3.5 $.

(1)将 $ A $,$ B $,$ C $,$ D $ 表示的数按从小到大的顺序用“＜”连接起来.
(2)若将原点改在 $ C $ 点,则 $ A $,$ B $,$ C $,$ D $ 点所对应的数分别为多少？将这些数按从小到大的顺序用“＜”连接起来.
(3)改变原点位置后,点 $ A $,$ B $,$ C $,$ D $ 所表示的数的大小顺序改变了吗？这说明了数轴的什么性质？

答案： 【解】
(1)根据数轴可知$-3＜-1.5＜2＜3.5$.
(2)若将原点改在C点,则点A表示的数为-3.5,点B表示的数为-5,点C表示的数为0,点D表示的数为1.5,则$-5＜-3.5＜0＜1.5$.
(3)由
(1)
(2)发现,改变原点位置后,点A,B,C,D所表示的数的大小顺序不会改变,这说明数轴上表示的两个数,右边的总比左边的大.