第79页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
1[2024甘肃张掖期末]为了迎接世界杯足球赛的到来,足球协会举办了一次足球赛,其中得分规则及奖励方案如表:
| |胜一场|平一场|负一场|
|积分(分)|3|1|0|
|人均奖金(元)|1500|700|0|
当比赛进行到每队比赛完12场时,A队共积分20分,并且没有负一场.
(1)试判断A队胜、平各几场.
(2)每赛一场,A队每名队员均得出场费500元,那么比赛完12场后,A队每名队员所得奖金与出场费累计为多少元?
| |胜一场|平一场|负一场|
|积分(分)|3|1|0|
|人均奖金(元)|1500|700|0|
当比赛进行到每队比赛完12场时,A队共积分20分,并且没有负一场.
(1)试判断A队胜、平各几场.
(2)每赛一场,A队每名队员均得出场费500元,那么比赛完12场后,A队每名队员所得奖金与出场费累计为多少元?
答案:
【解】
(1)设A队胜x场,则平(12 - x)场.由题意得3x+(12 - x)=20,解得x = 4,所以12 - x = 12 - 4 = 8.答:A队胜4场,平8场.
(2)因为每场比赛出场费500元,12场比赛出场费共6000元,赢了4场,奖金为1500×4 = 6000(元),平了8场,奖金为700×8 = 5600(元),所以奖金加出场费一共17600元.答:比赛完12场后,A队每名队员所得奖金与出场费累计为17600元.
(1)设A队胜x场,则平(12 - x)场.由题意得3x+(12 - x)=20,解得x = 4,所以12 - x = 12 - 4 = 8.答:A队胜4场,平8场.
(2)因为每场比赛出场费500元,12场比赛出场费共6000元,赢了4场,奖金为1500×4 = 6000(元),平了8场,奖金为700×8 = 5600(元),所以奖金加出场费一共17600元.答:比赛完12场后,A队每名队员所得奖金与出场费累计为17600元.
如图,等边三角形跑道的三个端点A,B,C上分别站着甲、乙、丙三人,其中甲的速度是丙的5倍.若三人同时顺时针出发,20分钟后甲首次追上丙,同时乙也首次追上了丙.若三人同时逆时针出发,甲首次追上丙和首次追上乙之间相差(
A.20分钟
B.30分钟
C.35分钟
D.40分钟
B
)A.20分钟
B.30分钟
C.35分钟
D.40分钟
答案:
B 【解析】设丙的速度为v,则甲的速度为5v.设乙的速度为v乙,等边三角形跑道的边长为a.由题意可得20(5v - v)=2a,20(v乙 - v)=a,解得a = 40v,v乙 = 3v.设甲追上乙需要t1分钟,由题意可得t1×(5v - 3v)=2a = 80v,解得t1 = 40.设甲追上丙需要t2分钟,由题意可得t2×(5v - v)=a = 40v,解得t2 = 10,所以甲首次追上丙和首次追上乙之间相差t1 - t2 = 40 - 10 = 30(分),故选B.
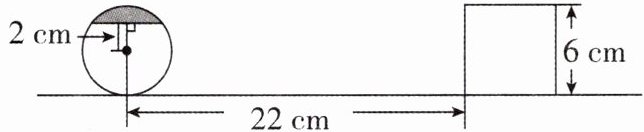
3[2024浙江宁波质检]如图,一个直径为6cm的圆中阴影部分面积为S,现在这个圆与正方形在同一平面内,沿同一条直线同时相向无滚动滑动.圆每秒滑动3cm,正方形每秒滑动2cm,第______秒时,圆与正方形重叠部分面积是S.

答案:
4或6 【解析】设第t秒时,圆与正方形重叠部分面积为S.当圆与正方形刚接触重叠时,如图
(1),根据题意,得2t+3t+2 = 22,解得t = 4;
当圆与正方形将要分开重叠时,如图
(2),根据题意,得2t+3t - (6 + 2)=22,解得t = 6.

综上,第4或6秒时,圆与正方形重叠部分面积为S.故答案为4或6.
4或6 【解析】设第t秒时,圆与正方形重叠部分面积为S.当圆与正方形刚接触重叠时,如图
(1),根据题意,得2t+3t+2 = 22,解得t = 4;

当圆与正方形将要分开重叠时,如图
(2),根据题意,得2t+3t - (6 + 2)=22,解得t = 6.

综上,第4或6秒时,圆与正方形重叠部分面积为S.故答案为4或6.
(1)B、C两地间的距离为
(2)A、B两地间的距离是
(x - 4)
km(用含有x的式子表示);(2)A、B两地间的距离是
47.5
km.
答案:
(1)(x - 4)
(2)47.5 【解析】
(1)因为A、C两地间的距离为4km,A、B两地间的距离为xkm,所以B、C两地的距离为(x - 4)km.故答案为(x - 4).
(2)由题意得$\frac{x}{16 + 4}+\frac{x - 4}{16 - 4}=6$,解得x = 47.5,所以A、B两地间的距离是47.5km.故答案为47.5.
(1)(x - 4)
(2)47.5 【解析】
(1)因为A、C两地间的距离为4km,A、B两地间的距离为xkm,所以B、C两地的距离为(x - 4)km.故答案为(x - 4).
(2)由题意得$\frac{x}{16 + 4}+\frac{x - 4}{16 - 4}=6$,解得x = 47.5,所以A、B两地间的距离是47.5km.故答案为47.5.
5[2025江苏南京期末]甲、乙两地相距600km,一辆客车从甲地开往乙地,速度为60km/h,一辆出租车从乙地开往甲地,速度为100km/h,两车同时出发,到达各自目的地后停止行驶.设客车行驶时间为t h.
(1)出发多长时间两车相遇(中途不停留)?
(2)分别写出t= 3,t= 5和t= 8时两车的距离(中途不停留);
(3)甲、乙两地之间有A、B两个加油站,相距200km,若客车进入A站加油时,出租车恰好进入B站加油.求A加油站到甲地的距离.
(1)出发多长时间两车相遇(中途不停留)?
(2)分别写出t= 3,t= 5和t= 8时两车的距离(中途不停留);
(3)甲、乙两地之间有A、B两个加油站,相距200km,若客车进入A站加油时,出租车恰好进入B站加油.求A加油站到甲地的距离.
答案:
【解】
(1)根据题意得60t+100t = 600,解得t = $\frac{15}{4}$,所以出发$\frac{15}{4}$h两车相遇.
(2)当t = 2时,两车相距600 - 2×(60 + 100)=280(km);当t = 5时,两车相距5×(60 + 100)-600 = 200(km);当t = 8时,出租车已经到达目的地,此时两车相距8×60 = 480(km).
(3)设A加油站到甲地的距离为xkm.当A加油站比B加油站更靠近甲地时,$\frac{x}{60}=\frac{600 - 200 - x}{100}$,解得x = 150;当A加油站比B加油站更靠近乙地时,$\frac{x}{60}=\frac{600 - x + 200}{100}$,解得x = 300,所以A加油站到甲地的距离为150km或300km.
(1)根据题意得60t+100t = 600,解得t = $\frac{15}{4}$,所以出发$\frac{15}{4}$h两车相遇.
(2)当t = 2时,两车相距600 - 2×(60 + 100)=280(km);当t = 5时,两车相距5×(60 + 100)-600 = 200(km);当t = 8时,出租车已经到达目的地,此时两车相距8×60 = 480(km).
(3)设A加油站到甲地的距离为xkm.当A加油站比B加油站更靠近甲地时,$\frac{x}{60}=\frac{600 - 200 - x}{100}$,解得x = 150;当A加油站比B加油站更靠近乙地时,$\frac{x}{60}=\frac{600 - x + 200}{100}$,解得x = 300,所以A加油站到甲地的距离为150km或300km.
查看更多完整答案,请扫码查看


