第58页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
我们用 $x_{n}$ 表示一个数列中的第 $n$ 个数,例如:$x_{1}$ 表示第一个数,$x_{2}$ 表示第二个数,$x_{3}$ 表示第三个数,…$$. 在某个数列中,若 $x_{1}= 3a - 3$,$x_{2}= 3 - 3b$,从第三个数开始,$x_{3}= x_{2}-x_{1}= (3 - 3b)-(3a - 3)= 6 - 3b - 3a$,$x_{4}= x_{3}-x_{2}= 6 - 3b - 3a-(3 - 3b)= 3 - 3a$,$x_{5}= x_{4}-x_{3}= 3 - 3a-(6 - 3b - 3a)= -3 + 3b$,…$$,下列三个说法:① $x_{7}= 3a - 3$;② $x_{2}+x_{23}= 0$;③ $x_{1}+x_{2}+x_{3}+… +x_{2024}= 3a - 3b$,其中说法正确的个数是(
A.0 个
B.1 个
C.2 个
D.3 个
D
)A.0 个
B.1 个
C.2 个
D.3 个
答案:
D [解析]x₆=x₅−x₄=(−3+3b)−(3−3a)=3a+3b−6,x₇=x₆−x₅=(3a+3b−6)−(−3+3b)=3a−3,故①正确.x₈=x₇−x₆=(3a−3)−(3a+3b−6)=3−3b,由上可知,xₙ每6个一循环.因为23÷6=3……5,所以x₂₃=x₅=−3+3b,所以x₂+x₂₃=3−3b+(−3+3b)=0,故②正确.因为x₁+x₂+x₃+x₄+x₅+x₆=(3a−3)+(3−3b)+(6−3b−3a)+(3−3a)+(−3+3b)+(3a+3b−6)=0,2024÷6=337……2,所以x₁+x₂+x₃+...+x₂₀₂₄=x₁+x₂=(3a−3)+(3−3b)=3a−3b,故③正确,综上,正确的个数是3个,故选D.
若关于 $x$,$y$ 的多项式 $(7mxy - 0.75y^{3})-2(2x^{2}y + 3xy)$ 化简后不含二次项,则 $m$ 的值为__
$\frac{6}{7}$
__.
答案:
$\frac{6}{7}$ [解析](7mxy−0.75y³)−2(2x²y+3xy)=7mxy−0.75y³−4x²y−6xy=−0.75y³+(7m−6)xy−4x²y;因为化简后不含二次项,所以7m−6=0,解得m=$\frac{6}{7}$.
3 [2025 湖南衡阳期中,中] 学习代数式求值时,经常会遇到这样一类题:“代数式 $ax - y + 6 + 3x - 5y - 1$ 的值与 $x$ 的取值无关,求 $a$ 的值”,通常的解题方法是把 $x$,$y$ 看作字母,$a$ 看作系数,合并同类项,即原式 $=(a + 3)x - 6y + 5$. 因为代数式的值与 $x$ 的取值无关,所以含 $x$ 项的系数为 0,所以 $a + 3 = 0$,则 $a = -3$.
(1)若关于 $x$ 的多项式 $(2x - 3)m + 2m^{2}-3x$ 的值与 $x$ 的取值无关,求 $m$ 的值;
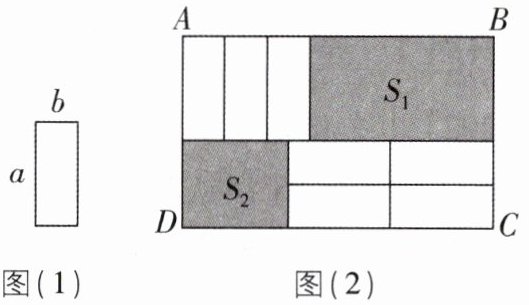
(2)7 张如图(1)的小长方形,长为 $a$,宽为 $b$,按照图(2)的方式不重叠地放在大长方形 $ABCD$ 内,设大长方形中未被覆盖的两个部分(图中阴影部分)中,右上角的面积为 $S_{1}$,左下角的面积为 $S_{2}$,当 $AB$ 的长变化时,$S_{1}-S_{2}$ 的值始终保持不变,求 $a$ 与 $b$ 的等量关系.
(1)若关于 $x$ 的多项式 $(2x - 3)m + 2m^{2}-3x$ 的值与 $x$ 的取值无关,求 $m$ 的值;
(2)7 张如图(1)的小长方形,长为 $a$,宽为 $b$,按照图(2)的方式不重叠地放在大长方形 $ABCD$ 内,设大长方形中未被覆盖的两个部分(图中阴影部分)中,右上角的面积为 $S_{1}$,左下角的面积为 $S_{2}$,当 $AB$ 的长变化时,$S_{1}-S_{2}$ 的值始终保持不变,求 $a$ 与 $b$ 的等量关系.

答案:
[解]
(1)(2x−3)m+2m²−3x=2mx−3m+2m²−3x=(2m−3)x+2m²−3m.因为其值与x的取值无关,所以2m−3=0,解得m=$\frac{3}{2}$.
(2)设AB=x,由题图可知S₁−S₂=(ax−3ab)−(2bx−4ab)=(a−2b)x+ab.因为当AB的长变化时,S₁−S₂的值始终保持不变,所以S₁−S₂ 的值与x的取值无关,所以a−2b=0,所以a=2b.
(1)(2x−3)m+2m²−3x=2mx−3m+2m²−3x=(2m−3)x+2m²−3m.因为其值与x的取值无关,所以2m−3=0,解得m=$\frac{3}{2}$.
(2)设AB=x,由题图可知S₁−S₂=(ax−3ab)−(2bx−4ab)=(a−2b)x+ab.因为当AB的长变化时,S₁−S₂的值始终保持不变,所以S₁−S₂ 的值与x的取值无关,所以a−2b=0,所以a=2b.
4 核心素养 运算能力 [中] 特殊值法,又叫特值法,是数学中通过设题中某个未知量为特殊值,从而通过简单的运算,得出最终答案的一种方法. 例如:
已知 $a_{4}x^{4}+a_{3}x^{3}+a_{2}x^{2}+a_{1}x + a_{0}= 6x$,则
① 取 $x = 0$ 时,直接可以得到 $a_{0}= 0$;
② 取 $x = 1$ 时,可以得到 $a_{4}+a_{3}+a_{2}+a_{1}+a_{0}= 6$;
③ 取 $x = -1$ 时,可以得到 $a_{4}-a_{3}+a_{2}-a_{1}+a_{0}= -6$;
④ 把②③中得出的结论相加,就可以得到 $2a_{4}+2a_{2}+2a_{0}= 0$,结合①中 $a_{0}= 0$ 的结论,即可得出 $a_{4}+a_{2}= 0$.
请类比上例,解决下面的问题:
已知 $a_{6}(x - 1)^{6}+a_{5}(x - 1)^{5}+a_{4}(x - 1)^{4}+a_{3}(x - 1)^{3}+a_{2}(x - 1)^{2}+a_{1}(x - 1)+a_{0}= 4x$,求:
(1)$a_{0}$ 的值;
(2)$a_{6}+a_{5}+a_{4}+a_{3}+a_{2}+a_{1}+a_{0}$ 的值;
(3)$a_{6}+a_{4}+a_{2}$ 的值.
已知 $a_{4}x^{4}+a_{3}x^{3}+a_{2}x^{2}+a_{1}x + a_{0}= 6x$,则
① 取 $x = 0$ 时,直接可以得到 $a_{0}= 0$;
② 取 $x = 1$ 时,可以得到 $a_{4}+a_{3}+a_{2}+a_{1}+a_{0}= 6$;
③ 取 $x = -1$ 时,可以得到 $a_{4}-a_{3}+a_{2}-a_{1}+a_{0}= -6$;
④ 把②③中得出的结论相加,就可以得到 $2a_{4}+2a_{2}+2a_{0}= 0$,结合①中 $a_{0}= 0$ 的结论,即可得出 $a_{4}+a_{2}= 0$.
请类比上例,解决下面的问题:
已知 $a_{6}(x - 1)^{6}+a_{5}(x - 1)^{5}+a_{4}(x - 1)^{4}+a_{3}(x - 1)^{3}+a_{2}(x - 1)^{2}+a_{1}(x - 1)+a_{0}= 4x$,求:
(1)$a_{0}$ 的值;
(2)$a_{6}+a_{5}+a_{4}+a_{3}+a_{2}+a_{1}+a_{0}$ 的值;
(3)$a_{6}+a_{4}+a_{2}$ 的值.
答案:
[解]
(1)当x=1时,a₀=4×1=4.
(2)当x=2时,可得a₆+a₅+a₄+a₃+a₂+a₁+a₀=4×2=8.
(3)当x=0时,可得a₆−a₅+a₄−a₃+a₂−a₁+a₀=0,①由
(2)得a₆+a₅+a₄+a₃+a₂+a₁+a₀=8,②①+②得2a₆+2a₄+2a₂+2a₀=8.因为a₀=4,所以2(a₆+a₄+a₂)=8−2×4=0,所以a₆+a₄+a₂=0.
(1)当x=1时,a₀=4×1=4.
(2)当x=2时,可得a₆+a₅+a₄+a₃+a₂+a₁+a₀=4×2=8.
(3)当x=0时,可得a₆−a₅+a₄−a₃+a₂−a₁+a₀=0,①由
(2)得a₆+a₅+a₄+a₃+a₂+a₁+a₀=8,②①+②得2a₆+2a₄+2a₂+2a₀=8.因为a₀=4,所以2(a₆+a₄+a₂)=8−2×4=0,所以a₆+a₄+a₂=0.
查看更多完整答案,请扫码查看


