第61页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
1 [2025安徽铜陵校级期中]在下面的月历表中,任意圈出一竖列上相邻的三个数,这三个数的和不可能是(
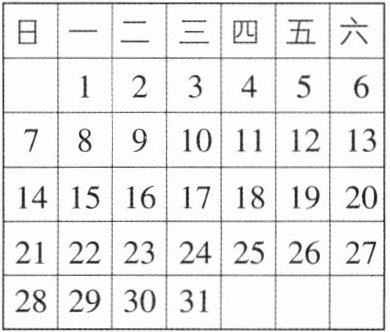
A.24
B.27
C.72
D.32
D
)
A.24
B.27
C.72
D.32
答案:
D 【解析】设中间的数为$x$,则上面的数为$x-7$,下面的数为$x+7$,则这三个数的和为$x-7+x+x+7=3x$,则这三个数的和必是3的倍数,故这三个数的和不可能为32.故选D.
如图是某月的月历,用“H”形框任意框中7个数(如阴影部分所示),则这7个数的和可能是____.(填写序号)
①55;②70;③84;④105;⑤140.
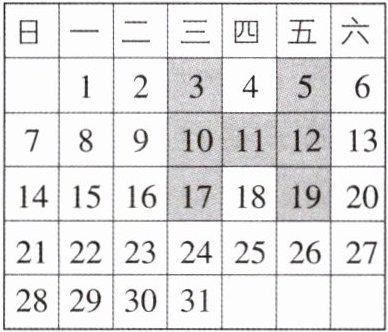
①55;②70;③84;④105;⑤140.

②③④
答案:
②③④ 【解析】设“H”形框框中的中间的数为$x$,所以其他几个数分别为$x-1$,$x+1$,$x-1-7=x-8$,$x+1-7=x-6$,$x+1+7=x+8$,$x-1+7=x+6$,所以这7个数的和为$x-1+x+1+x-8+x-6+x+8+x+6+x=7x$,所以这7个数的和是7的倍数,所以55不符合题意.因为$140÷7=20$,由题图可知“H”形框框中的中间的数不可能为20,所以140不符合题意,故只有②③④符合题意.故答案为②③④.
3 [2025河北石家庄质检]学习了整式的加减后,嘉淇发现任意三个连续奇数的和一定能被$n$($n$是大于1的整数)整除,关于结论Ⅰ、Ⅱ,下列判断正确的是(
结论Ⅰ:若设三个连续奇数中最小的奇数为$2m-1$,则这三个连续奇数的和为$6m+2$;
结论Ⅱ:$n的值为3$.
A.只有Ⅰ正确
B.只有Ⅱ正确
C.Ⅰ、Ⅱ都正确
D.Ⅰ、Ⅱ都不正确
B
)结论Ⅰ:若设三个连续奇数中最小的奇数为$2m-1$,则这三个连续奇数的和为$6m+2$;
结论Ⅱ:$n的值为3$.
A.只有Ⅰ正确
B.只有Ⅱ正确
C.Ⅰ、Ⅱ都正确
D.Ⅰ、Ⅱ都不正确
答案:
B 【解析】若设三个连续奇数中最小的奇数为$2m-1$,则另外两个奇数为$2m+1$,$2m+3$,所以这三个连续奇数的和为$2m-1+2m+1+2m+3=6m+3$,故Ⅰ错误.设三个连续奇数中中间的奇数为$x$,则最小的奇数为$x-2$,最大的奇数为$x+2$,所以这三个连续奇数的和为$x-2+x+x+2=3x$,所以这三个连续奇数的和一定能被3整除,所以$n$的值为3,故Ⅱ正确.故选B.
如果一个三位自然数,百位和个位上的数字之和为6,称这个数为“顺利数”,例如:145,因为$1+5= 6$,所以145是“顺利数”,则最大的“顺利数”是
690
;若“顺利数”$M$的十位数字比个位数字大2,$M去掉个位数字后所得的两位数与M$去掉百位数字后所得的两位数之和能被11整除,则$M$的值为353
.
答案:
690 353 【解析】因为一个三位自然数,百位和个位上的数字之和为6,称这个数为“顺利数”,所以“顺利数”的百位上的数字最大为6,则个位上的数字为0.若要使“顺利数”最大,则十位上的数字为9,所以最大的“顺利数”为690.设“顺利数”$M$为$100a+10b+c$,则$a+c=6$.因为“顺利数”$M$的十位数字比个位数字大2,所以$b-c=2$.因为$M$去掉个位数字后所得的两位数与$M$去掉百位数字后所得的两位数之和能被11整除,所以$10a+b+10b+c=10a+11b+c$能被11整除,所以$10a+c$能被11整除.因为$c=6-a$,所以$9a+6$能被11整除.因为$1\leqslant a\leqslant6$,所以$a=3$,所以$c=6-a=3$,所以$b=c+2=5$,所以“顺利数”$M$为353,故答案为690,353.
(1)填空:三位数$\overline{abc}=$
(2)试说明:$\overline{abc}-\overline{cba}$能被11整除;
(3)设$\overline{abcd}$是一个四位数,猜想$\overline{abcd}$满足什么条件时,它能被9整除,并说明理由.
$100a+10b+c$
;(2)试说明:$\overline{abc}-\overline{cba}$能被11整除;
【解】因为$\overline{abc}=100a+10b+c$,$\overline{cba}=100c+10b+a$,所以$\overline{abc}-\overline{cba}=100a+10b+c-(100c+10b+a)=99a-99c$.因为$99a-99c$能被11整除,所以$\overline{abc}-\overline{cba}$能被11整除.
(3)设$\overline{abcd}$是一个四位数,猜想$\overline{abcd}$满足什么条件时,它能被9整除,并说明理由.
【解】当$a+b+c+d$能被9整除时,$\overline{abcd}$能被9整除.理由:$\overline{abcd}=1000a+100b+10c+d=(999a+99b+9c)+(a+b+c+d)$.因为$999a+99b+9c$能被9整除,所以当$a+b+c+d$能被9整除时,$\overline{abcd}$能被9整除.
答案:
【解】
(1)$\overline{abc}=100a+10b+c$.故答案为$100a+10b+c$.
(2)因为$\overline{abc}=100a+10b+c$,$\overline{cba}=100c+10b+a$,所以$\overline{abc}-\overline{cba}=100a+10b+c-(100c+10b+a)=99a-99c$.因为$99a-99c$能被11整除,所以$\overline{abc}-\overline{cba}$能被11整除.
(3)当$a+b+c+d$能被9整除时,$\overline{abcd}$能被9整除.理由:$\overline{abcd}=1000a+100b+10c+d=(999a+99b+9c)+(a+b+c+d)$.因为$999a+99b+9c$能被9整除,所以当$a+b+c+d$能被9整除时,$\overline{abcd}$能被9整除.
(1)$\overline{abc}=100a+10b+c$.故答案为$100a+10b+c$.
(2)因为$\overline{abc}=100a+10b+c$,$\overline{cba}=100c+10b+a$,所以$\overline{abc}-\overline{cba}=100a+10b+c-(100c+10b+a)=99a-99c$.因为$99a-99c$能被11整除,所以$\overline{abc}-\overline{cba}$能被11整除.
(3)当$a+b+c+d$能被9整除时,$\overline{abcd}$能被9整除.理由:$\overline{abcd}=1000a+100b+10c+d=(999a+99b+9c)+(a+b+c+d)$.因为$999a+99b+9c$能被9整除,所以当$a+b+c+d$能被9整除时,$\overline{abcd}$能被9整除.
查看更多完整答案,请扫码查看


