《2025年拔尖特训八年级数学上册人教版》

8. 若 $ x ^ { 2 } - 2 ( 2024 - k ) x + 1 $ 是一个关于x的完全平方式，则k的值为2025 或 2023.

答案： 8. 2025 或 2023

9. （2025·眉山仁寿期中）已知 $ a = 2 ^ { 14 } $，$ b = 27 ^ { 5 } $，$ c = 9 ^ { 7 } $，则a，b，c的大小关系是（D）
A. $ a ＞ b ＞ c $
B. $ a ＞ c ＞ b $
C. $ a ＜ b ＜ c $
D. $ b ＞ c ＞ a $

答案： 9. D 解析：
∵ $ b = 27 ^ { 5 } = ( 3 ^ { 3 } ) ^ { 5 } = 3 ^ { 15 } $，$ c = 9 ^ { 7 } = ( 3 ^ { 2 } ) ^ { 7 } = 3 ^ { 14 } $，
∴ $ 2 ^ { 14 } ＜ 3 ^ { 14 } ＜ 3 ^ { 15 } $。
∴ $ b ＞ c ＞ a $。

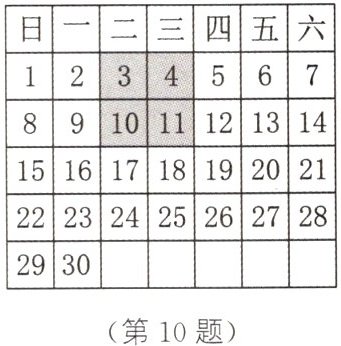
10. 如图所示为2025年6月的月历，现从中随机圈出四个数，对角线交叉相乘再相减，得 $ 4 × 10 - 3 × 11 = 40 - 33 = 7 $.进一步发现，从中随机抽出的四个数，若设 $ a = x $，用x表示b，c，d，得 $ b = $$ x + 1 $，$ c = $$ x + 7 $，$ d = $$ x + 8 $.于是 $ b c - a d = $$ ( x + 1 ) \cdot ( x + 7 ) - x ( x + 8 ) $.化简，得 $ b c - a d = $7.这就是隐含在月历中的秘密之一.

答案： 10. $ x + 1 $ $ x + 7 $ $ x + 8 $ $ ( x + 1 ) \cdot ( x + 7 ) - x ( x + 8 ) $ 7

11. 甲、乙两人计算 $ 2 ( x + a ) ( x + b ) $ 时，甲把第一个多项式中的a前面的符号错抄成了“ - ”，得到的结果为 $ 2 x ^ { 2 } + 6 x - 36 $；乙漏抄了2，得到的结果为 $ x ^ { 2 } + 9 x + 18 $.求：
（1）a，b的值.
（2）正确的结果.

答案： 11.
(1) 根据题意，得 $ 2 ( x - a ) ( x + b ) = 2 x ^ { 2 } + 2 b x - 2 a x - 2 a b = 2 x ^ { 2 } + ( 2 b - 2 a ) x - 2 a b = 2 x ^ { 2 } + 6 x - 36 $，$ ( x + a ) ( x + b ) = x ^ { 2 } + b x + a x + a b = x ^ { 2 } + ( a + b ) x + a b = x ^ { 2 } + 9 x + 18 $。
∴ $ 2 b - 2 a = 6 $，$ a + b = 9 $，解得 $ a = 3 $，$ b = 6 $。
(2) 把 $ a = 3 $，$ b = 6 $ 代入，得 $ 2 ( x + 3 ) ( x + 6 ) = 2 x ^ { 2 } + 12 x + 6 x + 36 = 2 x ^ { 2 } + 18 x + 36 $。

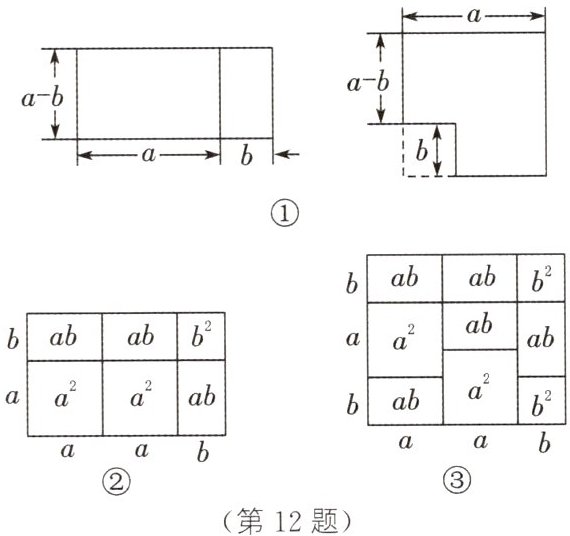
12. （2024·菏泽牡丹期末）探索有关整式的乘法法则时，可以借助几何图形来解释某些法则.例如：平方差公式可以用图①来解释.实际上还有些代数恒等式也可以用这种形式表示，例如：$ ( 2 a + b ) ( a + b ) = 2 a ^ { 2 } + 3 a b + b ^ { 2 } $ 就可以用图②中的几何图形的面积来表示.
（1）请写出图③中的几何图形所表示的代数恒等式：________________.
（2）试画出一个几何图形，使它的面积能表示 $ ( a + b ) ( a + 3 b ) = a ^ { 2 } + 4 a b + 3 b ^ { 2 } $.
（3）请仿照上述方法，另写一个含有a，b的代数恒等式，并画出与之相对应的几何图形.

答案：
12.
(1) $ ( 2 a + b ) ( a + 2 b ) = 2 a ^ { 2 } + 5 a b + 2 b ^ { 2 } $。
(2) 答案不唯一，如图①所示。
(3) 恒等式为 $ ( a + 2 b ) ( a + b ) = a ^ { 2 } + 3 a b + 2 b ^ { 2 } $，如图②所示（答案不唯一）。