《2025年拔尖特训八年级数学上册人教版》

1. 计算$8xy^{3}\cdot (-\frac {1}{4}x^{3}y^{2})$的结果为 （B）
A. $2x^{4}y^{5}$
B. $-2x^{4}y^{5}$
C. $2x^{3}y^{6}$
D. $-2x^{3}y^{5}$

答案： B

2. (2025·开封通许期中)下列计算正确的是 （B）
A. $6x^{2}\cdot 3xy=9x^{3}y^{3}$
B. $(2ab^{2})\cdot (-3ab)=-6a^{2}b^{3}$
C. $m^{2}n\cdot (-m^{2}n)=-m^{3}n^{3}$
D. $(-3x^{3}y)\cdot (-3xy)=9x^{3}y^{2}$

答案： B

3. (2025·泉州永春段考)$(4×10^{5})×(25×10^{3})$的计算结果是 （C）
A. $100×10^{8}$
B. $1×10^{17}$
C. $10^{10}$
D. $100×10^{15}$

答案： C

4. 计算：$(-3x^{2}y^{3})^{4}\cdot (-xy^{2})^{2}=$$81x^{10}y^{16}$。

答案： $81x^{10}y^{16}$

5. 光速约为$3×10^{5}km/s$，太阳系外距离地球最近的一颗恒星(比邻星)发出的光，需要大约4年的时间才能到达地球。若一年按$3×10^{7}s$计算，则这颗恒星到地球的距离约是$3.6×10^{13}$km。

答案： $3.6×10^{13}$

6. 已知$-2x^{3m+1}y^{2n}$与$4x^{n-6}y^{-3-m}$的积和$-4x^{4}y$是同类项，求m，n的值。

答案：
∵$-2x^{3m + 1}y^{2n}\cdot 4x^{n - 6}y^{-3 - m} = -8x^{3m + n - 5}y^{2n - 3 - m}$，$-2x^{3m + 1}y^{2n}$与$4x^{n - 6}y^{-3 - m}$的积和$-4x^{4}y$是同类项，
∴$\begin{cases}3m + n - 5 = 4\\2n - 3 - m = 1\end{cases}$，解得$\begin{cases}m = 2\\n = 3\end{cases}$。

7. 先化简，再求值：$2x^{2}y\cdot (-2xy^{2})^{3}+(2xy)^{3}\cdot (-xy^{2})^{2}$，其中$x=4,y=\frac {1}{4}$。

答案： 原式$= 2x^{2}y\cdot (-8x^{3}y^{6}) + 8x^{3}y^{3}\cdot x^{2}y^{4} = -16x^{5}y^{7} + 8x^{5}y^{7} = -8x^{5}y^{7}$。
当$x = 4$，$y = \frac{1}{4}$时，原式$= -8×(xy)^{5}\cdot y^{2} = -8×(4×\frac{1}{4})^{5}×(\frac{1}{4})^{2} = -8×\frac{1}{16} = -\frac{1}{2}$。

8. 若$(-2x^{2}y^{3})^{m}\cdot (xy)^{n}=ax^{7}y^{9}$，则常数a的值为 （C）
A. 8
B. -8
C. 4
D. -4

答案： C

9. (2025·海口龙华期中)若单项式$-4x^{a}y$和$\frac {1}{2}x^{2}y^{b}$的积为$-2x^{7}y^{6}$，则ab的算术平方根为 （C）
A. $\sqrt {5}$
B. $\sqrt {15}$
C. 5
D. 10

答案： C解析：$-4x^{a}y\cdot \frac{1}{2}x^{2}y^{b} = -2x^{a + 2}y^{1 + b} = -2x^{7}y^{6}$，
∴$a + 2 = 7$，$1 + b = 6$，解得$a = 5$，$b = 5$。
∴$\sqrt{ab} = \sqrt{25} = 5$。

10. 已知$a^{m}=7,b^{n}=\frac {1}{7}$，则$(-a^{3m}b^{n})^{2}\cdot (a^{m}b^{2n})^{3}$的值为 （C）
A. 1
B. -1
C. 7
D. $\frac {1}{7}$

答案： C解析：$(-a^{3m}b^{n})^{2}\cdot (a^{m}b^{2n})^{3} = (a^{m})^{6}\cdot (b^{n})^{2}\cdot (a^{m})^{3}\cdot (b^{n})^{6} = (a^{m})^{9}\cdot (b^{n})^{8} = 7^{9}×(\frac{1}{7})^{8} = 7^{8}×(\frac{1}{7})^{8}×7 = (7×\frac{1}{7})^{8}×7 = 7$。

11. (2025·江门期中)已知$m+2n-2=0$，则$2^{m}\cdot 4^{n}$的值为4。

答案： 4

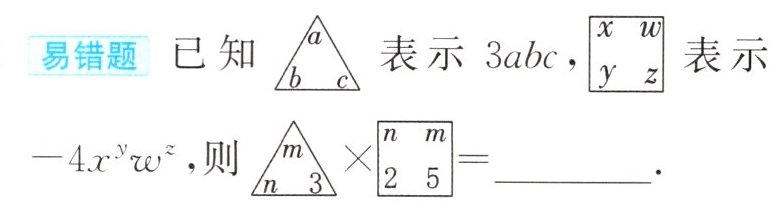
12. 

答案：
$-36m^{6}n^{3}$ 解析：根据题意，得$ = 9mn×(-4n^{2}m^{5}) = -36m^{6}n^{3}$。
易错警示：单项式与单项式相乘时，应注意不要漏乘只在一个单项式中出现的字母，且应先确定积的符号。

13. 若$ab^{2}=-1$，则$2a^{2}b\cdot 3ab^{5}=$$-6$。

答案： $-6$