《2025年拔尖特训八年级数学上册人教版》

典例1 如图，△ACD和△ECB分别与△ACB成轴对称，对称轴分别是直线AC，BC。如果AD⊥BE，那么∠DCE的度数为________。

答案：
$45^{\circ}$ 解析: 如图, 设 $AD$ 与 $BE$ 的交点为 $O$. $\because \triangle ACD$ 和 $\triangle ECB$ 分别与 $\triangle ACB$ 成轴对称, $\therefore \angle BAC=\angle DAC$, $\angle ABC=\angle EBC$. 由三角形内角和定理, 得 $\angle AOB+\angle BAD+\angle ABE=180^{\circ}$. $\because AD\perp BE$, 即 $\angle AOB=90^{\circ}$, $\therefore \angle BAD+\angle ABE=90^{\circ}$. $\therefore \angle BAC+\angle ABC=45^{\circ}$. $\therefore \angle ACB=180^{\circ}-45^{\circ}=135^{\circ}$. $\therefore$ 易得 $\angle ACB=\angle ACD=\angle BCE=135^{\circ}$. $\therefore \angle DCE=135^{\circ}\times 3-360^{\circ}=45^{\circ}$.
　　　　

[变式] 如图，分别以△ABC的边AB，AC所在的直线为对称轴作△ABC的对称图形△ABD和△AEC，∠BAC=150°，线段BD与CE相交于点O，连接BE，ED，DC，OA。有下列结论：①∠EAD=90°；②∠BOE=60°；③OA平分∠BOC；④BP=EQ。其中，正确的是________(填序号)。
[img]

①②③

答案： ①②③

典例2 如图，M是线段AD，CD的垂直平分线的交点，AB⊥BC，∠D=65°，则∠MAB+∠MCB的度数是()

A. 120°
B. 130°
C. 140°
D. 160°

答案：
C 解析: 如图, 过点 $M$ 作射线 $DN$. $\because M$ 是线段 $AD$, $CD$ 的垂直平分线的交点, $\therefore AM=DM$, $CM=DM$. $\therefore \angle DAM=\angle ADM$, $\angle DCM=\angle CDM$. $\therefore \angle MAD+\angle MCD=\angle ADM+\angle CDM=\angle ADC=65^{\circ}$. $\therefore \angle AMC=\angle AMN+\angle CMN=\angle MAD+\angle ADM+\angle MCD+\angle CDM=65^{\circ}+65^{\circ}=130^{\circ}$. $\because AB\perp BC$, $\therefore \angle B=90^{\circ}$. $\therefore \angle MAB+\angle MCB=360^{\circ}-\angle B-\angle AMC=360^{\circ}-90^{\circ}-130^{\circ}=140^{\circ}$.
　　　　　

[变式] 如图，在四边形ABCD中，AE，AF分别是BC，CD的垂直平分线，∠EAF=75°，∠CBD=35°，则∠ADC的度数为(A)
A. 55°
B. 60°
C. 80°
D. 100°

答案： A 解析: 连接 $AC$. $\because AE$, $AF$ 分别是 $BC$, $CD$ 的垂直平分线, $\therefore AB=AC=AD$. $\because AF\perp DC$, $AE\perp BC$, $\therefore \angle CAF=\angle DAF$, $\angle CAE=\angle BAE$. $\therefore$ 易得 $\angle DAB=2\angle EAF=150^{\circ}$. $\therefore \angle ABD=\angle ADB=(180^{\circ}-150^{\circ})\div 2=15^{\circ}$. $\therefore \angle ABC=\angle ACB=\angle CBD+\angle ABD=35^{\circ}+15^{\circ}=50^{\circ}$. $\because$ 在四边形 $AECF$ 中, $\angle FCE=360^{\circ}-90^{\circ}-90^{\circ}-75^{\circ}=105^{\circ}$, $\therefore \angle ACD=105^{\circ}-50^{\circ}=55^{\circ}$. $\therefore \angle ADC=\angle ACD=55^{\circ}$.

典例3 (2025·金华义乌段考)如图，在△ABC中，∠B=∠C，点D在BC上，点E在AC上，连接AD，DE且∠ADE=∠AED。当点D在边BC(不与点B，C重合)上运动时，且点E在边AC上，猜想∠BAD与∠CDE的数量关系，并加以证明。

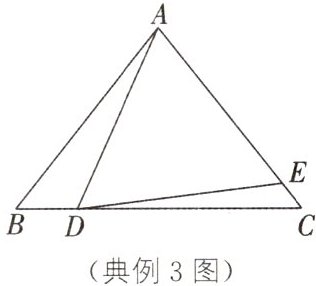
答案： $\angle BAD=2\angle CDE$.
设 $\angle B=x$, $\angle ADE=y$,
$\because \angle B=\angle C$,
$\therefore \angle C=x$.
$\because \angle AED=\angle ADE$,
$\therefore \angle AED=y$.
$\therefore \angle CDE=\angle AED-\angle C=y-x$, $\angle DAE=180^{\circ}-\angle ADE-\angle AED=180^{\circ}-2y$.
$\therefore \angle BAD=180^{\circ}-\angle B-\angle C-\angle DAE=180^{\circ}-x-x-(180^{\circ}-2y)=2(y-x)$.
$\therefore \angle BAD=2\angle CDE$.

(1)当DE//BC时，△ACD按角分类是直角三角形。
(2)在点D运动的过程中，△ECD可以是等腰三角形吗？若可以，请求出∠AED的度数；若不可以，请说明理由。
△ECD可以是等腰三角形，此时∠AED的度数为60°或105°。

答案：
(1) 直角三角形.
解析: $\because$ 在 $\triangle ABC$ 中, $AC=BC$, $\therefore \angle A=\angle B=\frac{180^{\circ}-\angle ACB}{2}=\frac{180^{\circ}-120^{\circ}}{2}=30^{\circ}$. $\because DE// BC$, $\therefore \angle ADE=\angle B=30^{\circ}$. 又 $\because \angle CDE=30^{\circ}$, $\therefore \angle ADC=\angle ADE+\angle CDE=30^{\circ}+30^{\circ}=60^{\circ}$. $\therefore \angle ACD=180^{\circ}-\angle A-\angle ADC=180^{\circ}-30^{\circ}-60^{\circ}=90^{\circ}$. $\therefore \triangle ACD$ 是直角三角形.
(2) $\triangle ECD$ 可以是等腰三角形.
分三种情况讨论:
① 当 $\angle CDE=\angle ECD$ 时, $ED=EC$, $\therefore \angle ECD=\angle CDE=30^{\circ}$. $\because \angle AED=\angle ECD+\angle CDE$, $\therefore \angle AED=60^{\circ}$.
② 当 $\angle ECD=\angle CED$ 时, $CD=DE$, $\because \angle ECD+\angle CED+\angle CDE=180^{\circ}$, $\therefore \angle CED=\frac{180^{\circ}-\angle CDE}{2}=\frac{180^{\circ}-30^{\circ}}{2}=75^{\circ}$. $\therefore \angle AED=180^{\circ}-\angle CED=105^{\circ}$.
③ 当 $\angle CED=\angle CDE$ 时, $EC=CD$, $\angle ACD=180^{\circ}-\angle CED-\angle CDE=180^{\circ}-30^{\circ}-30^{\circ}=120^{\circ}$. $\because \angle ACB=120^{\circ}$, $\therefore$ 此时点 $D$ 与点 $B$ 重合, 不合题意.
综上所述, $\triangle ECD$ 可以是等腰三角形, 此时 $\angle AED$ 的度数为 $60^{\circ}$ 或 $105^{\circ}$.