第50页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
1. 如图,在$\triangle ABC$中,$AB=AC$,$BD$平分$\angle ABC$交$AC$于点$G$,$DM// BC$交$\triangle ABC$的外角的平分线于点$M$,交$AB$,$AC$于点$F$,$E$。下列结论中,正确的是()
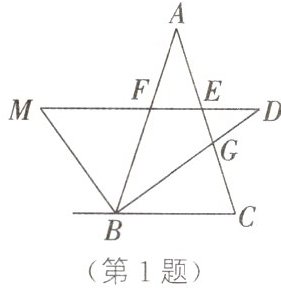
A. $EF=ED$
B. $FD=BC$
C. $EC=MF$
D. $EC=AG$

A. $EF=ED$
B. $FD=BC$
C. $EC=MF$
D. $EC=AG$
答案:
C
方法归纳
角平分线和平行线构造等腰三角形模型
常见的角平分线和平行线构造等腰三角形模型有以下四种:

C
方法归纳
角平分线和平行线构造等腰三角形模型
常见的角平分线和平行线构造等腰三角形模型有以下四种:

2. 如图,在$\triangle ABC$中,$\angle ABC$的平分线交$AC$于点$D$,$AD=6$,过点$D$作$DE// BC$,交$AB$于点$E$。若$\triangle AED$的周长为$16$,则边$AB$的长为______
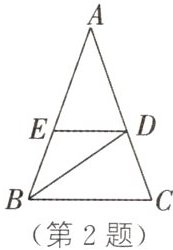
10
。
答案:
10
3. 如图,在$\triangle ABC$中,$\angle A=\angle ABE$,$CD$平分$\angle BCE$,且$CD\perp BE$于点$D$,$AC=5$,$BC=3$,则$DE$的长为
1
。
答案:
1
4. 如图,在$\triangle ABC$中,$AB=AC$。过点$A$作$AD// BC$,交$\angle ACB$的平分线于点$D$,连接$BD$。
(1)求证:$\triangle ABD$是等腰三角形。
(2)若$\angle BDC=20^{\circ}$,求$\angle ADC$的度数。
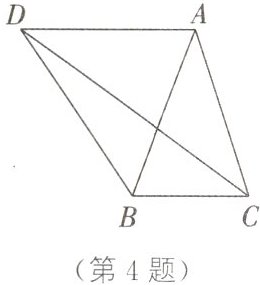
(1)求证:$\triangle ABD$是等腰三角形。
(2)若$\angle BDC=20^{\circ}$,求$\angle ADC$的度数。

答案:
(1)
∵AD//BC,
∴∠ADC=∠DCB.
∵CD平分∠ACB,
∴∠ACD=∠DCB.
∴∠ADC=∠ACD.
∴AD=AC.
∵AB=AC,
∴AD=AB.
∴△ABD是等腰三角形.
(2)设∠ADC=x.
由
(1),可得∠ADC=∠ACD=∠DCB=x.
∴∠ACB=∠ACD+∠DCB=2x.
∵AB=AC,
∴∠ABC=∠ACB=2x.
∵∠BDC=20°,
∴∠ADB=∠ADC+∠BDC=x+20°.
∵AD=AB,
∴∠ADB=∠ABD=x+20°.
∵∠BDC+∠DBC+∠DCB=180°,
∴∠BDC+∠ABD+∠ABC+∠DCB=180°.
∴20°+x+20°+2x+x=180°,解得x=35°.
∴∠ADC=35°.
(1)
∵AD//BC,
∴∠ADC=∠DCB.
∵CD平分∠ACB,
∴∠ACD=∠DCB.
∴∠ADC=∠ACD.
∴AD=AC.
∵AB=AC,
∴AD=AB.
∴△ABD是等腰三角形.
(2)设∠ADC=x.
由
(1),可得∠ADC=∠ACD=∠DCB=x.
∴∠ACB=∠ACD+∠DCB=2x.
∵AB=AC,
∴∠ABC=∠ACB=2x.
∵∠BDC=20°,
∴∠ADB=∠ADC+∠BDC=x+20°.
∵AD=AB,
∴∠ADB=∠ABD=x+20°.
∵∠BDC+∠DBC+∠DCB=180°,
∴∠BDC+∠ABD+∠ABC+∠DCB=180°.
∴20°+x+20°+2x+x=180°,解得x=35°.
∴∠ADC=35°.
5. 如图,在$\triangle ABC$中,$AB=AC$,点$M$在$CA$的延长线上,$MN\perp BC$于点$N$,交$AB$于点$O$。若$AO=3$,$BO=4$,则$MC$的长为(
A. $12$
B. $9$
C. $10$
D. $11$
C
)A. $12$
B. $9$
C. $10$
D. $11$
答案:
5.C 解析:
∵AB=AC,
∴∠B=∠C.
∵MN⊥BC,
∴∠MNC=∠MNB=90°,
∴∠B+∠BON=90°,∠C+∠M=90°.
∴∠M=∠BON.
∵ ∠BON=∠MOA,
∴∠M=∠MOA.
∴AM=AO=3.
∵BO=4,
∴AB=AC=AO+BO=7.
∴MC=AM+AC=10.
∵AB=AC,
∴∠B=∠C.
∵MN⊥BC,
∴∠MNC=∠MNB=90°,
∴∠B+∠BON=90°,∠C+∠M=90°.
∴∠M=∠BON.
∵ ∠BON=∠MOA,
∴∠M=∠MOA.
∴AM=AO=3.
∵BO=4,
∴AB=AC=AO+BO=7.
∴MC=AM+AC=10.
6. (2025·泰州靖江段考)如图,$AB// CD$,$\angle BAC$的平分线与$CD$交于点$E$,$F$为射线$AB$上的一个动点,连接$EF$,过点$C$作$CG\perp EF$于点$G$。若$FG=EG$,$\angle BAC=70^{\circ}$,则$\angle AEF$的度数为(
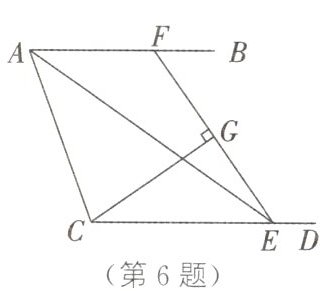
A. $10^{\circ}$
B. $20^{\circ}$
C. $25^{\circ}$
D. $35^{\circ}$
B
)
A. $10^{\circ}$
B. $20^{\circ}$
C. $25^{\circ}$
D. $35^{\circ}$
答案:
6.B
7. 在如图所示的$5$个三角形中,均有$AB=AC$,经过三角形一个顶点的一条直线不能将这个三角形分成两个小等腰三角形的为
②⑤
(填序号)。
答案:
7.②⑤ 解析:①如图①,过点B作∠ABC的平分线,交AC于点D.
∵AB=AC,∠A=36°,
∴易得∠ABC=∠C=72°.
∴∠ABD=∠CBD=$\frac{1}{2}$∠ABC=36°=∠A.
∴BD=AD,∠BDC=36°+36°=72°,
∴∠BDC=∠C.
∴BD=BC.
∴△ABD和△BCD是等腰三角形.
∴能将这个三角形分成两个小等腰三角形.②不能将这个三角形分成两个小等腰三角形.③如图②,过点A作∠BAC的平分线,交BC于点D.
∴∠BAD=∠CAD=$\frac{1}{2}$∠BAC=45°.
∵∠BAC=90°,AB=AC,
∴易得∠B=∠C=45°.
∴易得△ABD和△ACD是等腰三角形.
∴能将这个三角形分成两个小等腰三角形.④如图③,过点A把∠BAC分成36°和72°两个角,则∠BAD=36°,∠CAD=72°.
∵∠BAC=108°,AB=AC,
∴易得∠B=∠C=36°.
∴∠BAD=∠B,易得∠ADC=∠CAD.
∴易得△ABD和△ACD是等腰三角形.
∴能将这个三角形分成两个小等腰三角形.⑤不能将这个三角形分成两个小等腰三角形.综上所述,不能将这个三角形分成两个小等腰三角形的为②⑤.
∵AB=AC,∠A=36°,
∴易得∠ABC=∠C=72°.
∴∠ABD=∠CBD=$\frac{1}{2}$∠ABC=36°=∠A.
∴BD=AD,∠BDC=36°+36°=72°,
∴∠BDC=∠C.
∴BD=BC.
∴△ABD和△BCD是等腰三角形.
∴能将这个三角形分成两个小等腰三角形.②不能将这个三角形分成两个小等腰三角形.③如图②,过点A作∠BAC的平分线,交BC于点D.
∴∠BAD=∠CAD=$\frac{1}{2}$∠BAC=45°.
∵∠BAC=90°,AB=AC,
∴易得∠B=∠C=45°.
∴易得△ABD和△ACD是等腰三角形.
∴能将这个三角形分成两个小等腰三角形.④如图③,过点A把∠BAC分成36°和72°两个角,则∠BAD=36°,∠CAD=72°.
∵∠BAC=108°,AB=AC,
∴易得∠B=∠C=36°.
∴∠BAD=∠B,易得∠ADC=∠CAD.
∴易得△ABD和△ACD是等腰三角形.
∴能将这个三角形分成两个小等腰三角形.⑤不能将这个三角形分成两个小等腰三角形.综上所述,不能将这个三角形分成两个小等腰三角形的为②⑤.
8. 如图,$CE$平分$\angle ACB$,且$CE\perp DB$于点$E$,$\angle DAB=\angle DBA$。若$AC=14$,$\triangle CDB$的周长为$20$,则$BD$的长为______
8
。
答案:
8.8 解析:
∵CE⊥DB,
∴∠CED=∠CEB=90°.
∵CE平分∠ACB,
∴∠DCE=∠BCE.
∴∠CDE=∠CBE.
∴CD=CB.
∵∠DAB=∠DBA,
∴AD=BD.
∵△CDB的周长为20,
∴CD+CB+BD=20.
∵AC=14,
∴AD+CD=14.
∴BD+CD=14.
∴CB=20−14=6.
∴CD=CB=6.
∴BD=AD=14−6=8.
∵CE⊥DB,
∴∠CED=∠CEB=90°.
∵CE平分∠ACB,
∴∠DCE=∠BCE.
∴∠CDE=∠CBE.
∴CD=CB.
∵∠DAB=∠DBA,
∴AD=BD.
∵△CDB的周长为20,
∴CD+CB+BD=20.
∵AC=14,
∴AD+CD=14.
∴BD+CD=14.
∴CB=20−14=6.
∴CD=CB=6.
∴BD=AD=14−6=8.
查看更多完整答案,请扫码查看


