《2025年拔尖特训八年级数学上册人教版》

10. （2024·东莞期末）已知$a$，$b$，$c$是$\triangle ABC$的三边长，且$\vert a-3\vert +(b-4)^{2}=0$.
（1）求$a$，$b$的值以及$c$的取值范围.
（2）若$\triangle ABC$是等腰三角形，求此三角形的周长.
（3）若在另一个等腰三角形$DEF$中，一个内角为$x^{\circ}$，另一个内角为$(2x-20)^{\circ}$，求此三角形各内角的度数.

答案：
(1)$\because |a - 3|+(b - 4)^{2}=0$，$\therefore a = 3$，$b = 4$。$\because b - a\lt c\lt b + a$，$\therefore 1\lt c\lt 7$。
(2)当腰长为$3$时，此时三角形的三边长为$3$，$3$，$4$，满足三角形的三边关系，周长为$10$。当腰长为$4$时，此时三角形的三边长为$4$，$4$，$3$，满足三角形的三边关系，周长为$11$。综上所述，此三角形的周长为$10$或$11$。
(3)当底角为$x^{\circ}$、顶角为$(2x - 20)^{\circ}$时，则根据三角形内角和为$180^{\circ}$可得$x + x + 2x - 20 = 180$，解得$x = 50$，此时三个内角的度数分别为$50^{\circ}$，$50^{\circ}$，$80^{\circ}$。当顶角为$x^{\circ}$、底角为$(2x - 20)^{\circ}$时，则根据三角形内角和为$180^{\circ}$可得$x + 2x - 20 + 2x - 20 = 180$，解得$x = 44$，此时三个内角的度数分别为$44^{\circ}$，$68^{\circ}$，$68^{\circ}$。当底角为$x^{\circ}$、$(2x - 20)^{\circ}$时，则根据等腰三角形的性质可得$x = 2x - 20$，解得$x = 20$，此时三个内角的度数分别为$20^{\circ}$，$20^{\circ}$，$140^{\circ}$。综上所述，此三角形三个内角的度数分别为$50^{\circ}$，$50^{\circ}$，$80^{\circ}$或$44^{\circ}$，$68^{\circ}$，$68^{\circ}$或$20^{\circ}$，$20^{\circ}$，$140^{\circ}$。

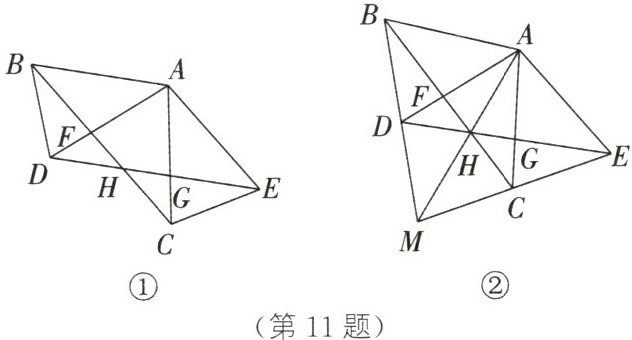
11. 如图①，$\triangle ABC$和$\triangle ADE$都是等腰三角形，$\angle BAC=\angle DAE=100^{\circ}$，$AB=AC=AD=AE$，$BC$与$AD$，$DE$分别交于点$F$，$H$，$AC$与$DE$交于点$G$，连接$BD$，$CE$.
（1）若$\angle DBA=70^{\circ}$，求$\angle DAC$的度数.
（2）如图②，延长$BD$，$EC$交于点$M$，连接$MH$，$AH$. 求证：$A$，$H$，$M$三点在同一条直线上.

答案：

(1)$\because AB = AD$，$\angle DBA = 70^{\circ}$，$\therefore \angle ABD=\angle BDA = 70^{\circ}$。$\therefore \angle BAD = 180^{\circ}-2\times70^{\circ}=40^{\circ}$。$\because \angle BAC = 100^{\circ}$，$\therefore \angle DAC = 100^{\circ}-40^{\circ}=60^{\circ}$。
(2)如图，连接$BE$。在$\triangle ABC$和$\triangle ADE$中，$\because \angle BAC=\angle DAE = 100^{\circ}$，$AB = AD$，$AC = AE$，$\therefore \triangle ABC\cong\triangle ADE$。$\therefore$易得$\angle ABC=\angle ACB=\angle ADE=\angle AED = 40^{\circ}$，$BC = DE$。$\because \angle BAC=\angle DAE = 100^{\circ}$，$\therefore$易得$\angle BAD=\angle CAE$。又$\because AB = AC = AD = AE$，$\therefore \triangle ABD\cong\triangle ACE$。$\therefore BD = CE$，$\angle ABD=\angle ADB=\angle ACE=\angle AEC$。$\because \angle DBH=\angle ABD-\angle ABC$，$\angle CEH=\angle AEC-\angle AED$，$\therefore \angle DBH=\angle CEH$。又$\because \angle DHB=\angle CHE$，$BD = EC$，$\therefore \triangle DBH\cong\triangle CEH$。$\therefore BH = EH$。$\because \angle MDE+\angle ADB+\angle ADE = 180^{\circ}$，$\angle MCB+\angle ACE+\angle ACB = 180^{\circ}$，$\therefore \angle MDE=\angle MCB$。又$\because DE = CB$，$\angle MED=\angle MBC$，$\therefore \triangle MDE\cong\triangle MCB$。$\therefore ME = MB$。$\because AB = AE$，$BH = EH$，$\therefore A$，$H$，$M$三点在线段$BE$的垂直平分线上。$\therefore A$，$H$，$M$三点在同一条直线上。