第65页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
1. (2023·秦皇岛期末)如图所示为钝角三角形ABC,按以下步骤进行尺规作图,并保留作图痕迹。步骤1:以点C为圆心,CB长为半径画弧;步骤2:以点A为圆心,AB长为半径画弧,两弧交于点D;步骤3:连接BD,交AC的延长线于点E。下列叙述中,正确的是(
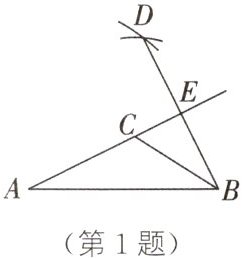
A. BC平分∠ABD
B. AB=BD
C. AE=BD
D. BE=DE
D
)
A. BC平分∠ABD
B. AB=BD
C. AE=BD
D. BE=DE
答案:
D
2. 在等腰三角形ABC中,AD是△ABC的高。若AD=1/2BC,则△ABC的底角的度数为(
A. 15°或45°
B. 30°或90°
C. 30°或60°或90°
D. 15°或45°或75°
D
)A. 15°或45°
B. 30°或90°
C. 30°或60°或90°
D. 15°或45°或75°
答案:
D
3. 如图,△ABC的三条高相交于点G,CH是△ABC的角平分线,CH与BE相交于点I,AD与CH相交于点J,∠ABC=45°,∠ACD=60°,则图中的等腰三角形共有(
A. 5个
B. 6个
C. 7个
D. 8个
D
)A. 5个
B. 6个
C. 7个
D. 8个
答案:
D 解析: ① $\because AD\perp BC$, $\angle ABC=45^{\circ}$, $\therefore$ 易得 $\triangle ABD$ 是等腰三角形. ② $\because CF\perp AB$, $\angle ABC=45^{\circ}$, $\therefore$ 易得 $\triangle BCF$ 是等腰三角形. ③ $\because \angle ACB=60^{\circ}$, $\therefore \angle CBE=90^{\circ}-60^{\circ}=30^{\circ}$. $\because CH$ 是 $\triangle ABC$ 的角平分线, $\therefore \angle BCH=\angle ACH=\frac{1}{2}\angle ACB=30^{\circ}$. $\therefore \angle CBI=\angle ICB$. $\therefore \triangle BCI$ 是等腰三角形. ④ $\because \angle ACB=60^{\circ}$, $\therefore \angle CAD=90^{\circ}-60^{\circ}=30^{\circ}$. $\therefore$ 易得 $\angle ACJ=\angle CAJ=30^{\circ}$. $\therefore \triangle ACJ$ 是等腰三角形. ⑤ $\because \angle ACF=60^{\circ}-45^{\circ}=15^{\circ}$, $\therefore \angle CAF=90^{\circ}-15^{\circ}=75^{\circ}$. $\therefore \angle AHC=\angle ABC+\angle BCH=45^{\circ}+30^{\circ}=75^{\circ}$. $\therefore \angle CAH=\angle CHA=75^{\circ}$. $\therefore \triangle ACH$ 是等腰三角形. ⑥ $\because \angle GCD=45^{\circ}$, $\angle GDC=90^{\circ}$, $\therefore \angle DGC=45^{\circ}$. $\therefore \angle GCD=\angle DGC$. $\therefore \triangle CDG$ 是等腰三角形. ⑦ $\because \angle GIJ=\angle EBC+\angle HCB=30^{\circ}+30^{\circ}=60^{\circ}$, $\angle GJI=\angle CJD=90^{\circ}-30^{\circ}=60^{\circ}$, $\therefore \angle GIJ=\angle GJI=60^{\circ}$. $\therefore \triangle GIJ$ 是等腰三角形. ⑧ $\because \angle FAG=\angle CAH-\angle CAD=75^{\circ}-30^{\circ}=45^{\circ}$, $\angle FGA=\angle DGC=45^{\circ}$, $\therefore \angle FAG=\angle FGA$. $\therefore \triangle AFG$ 是等腰三角形. 综上所述, 图中的等腰三角形共有 $8$ 个.
4. 如图,在△ABC中,AC=BC,AB=6,△ABC的面积为12,CD⊥AB于点D,直线EF垂直平分BC,交AB于点E,交BC于点F,P是线段EF上的一个动点,则△PBD的周长的最小值是(
A. 6
B. 7
C. 10
D. 12
B
)A. 6
B. 7
C. 10
D. 12
答案:
B
5. 如图,△ABC是等边三角形,BD=CD,E是边AC上的点,DE//AB,与BC交于点F。有下列结论:①连接AD,则AD垂直平分线段BC;②△CEF是等边三角形;③若AB=8,CE=2,则CF=4;④若∠CBD=40°,则∠EDC=10°。其中,正确的是
[img]
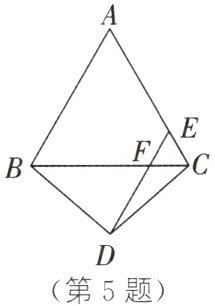
①②
(填序号)。[img]

答案:
①②
6. 如图,在△ABC中,∠B=2∠C,AE为边BC上的高。若BE=1,AB=4,则BC的长为________。
[img]
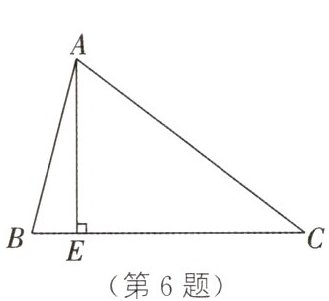
[img]

答案:
6 解析: 如图, 在 $CE$ 上截取 $EF=BE=1$, 连接 $AF$. $\because AE\perp BF$, $\therefore$ 易得 $AB=AF=4$. $\therefore \angle B=\angle AFB$. $\because \angle AFB=\angle C+\angle CAF$, $\therefore \angle B=\angle C+\angle CAF$. $\because \angle B=2\angle C$, $\therefore \angle C=\angle CAF$. $\therefore CF=AF=4$. $\therefore BC=BE+EF+CF=6$.

6 解析: 如图, 在 $CE$ 上截取 $EF=BE=1$, 连接 $AF$. $\because AE\perp BF$, $\therefore$ 易得 $AB=AF=4$. $\therefore \angle B=\angle AFB$. $\because \angle AFB=\angle C+\angle CAF$, $\therefore \angle B=\angle C+\angle CAF$. $\because \angle B=2\angle C$, $\therefore \angle C=\angle CAF$. $\therefore CF=AF=4$. $\therefore BC=BE+EF+CF=6$.

7. (2024·眉山东坡期末)如图,在等边三角形ABC中,AD为边BC上的高,点M,N分别在AD,AC上,且AM=CN,连接BM,BN。当BM+BN的值最小时,∠MBN=________。
[img]
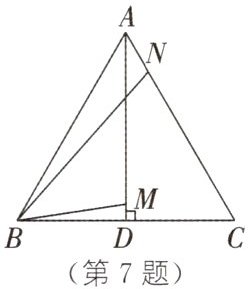
[img]

答案:
$30^{\circ}$ 解析: 如图①, 过点 $C$ 作 $CH\perp BC$, 使得 $CH=BC$, 连接 $NH$, $BH$. $\because \triangle ABC$ 是等边三角形, $AD\perp BC$, $CH\perp BC$, $\therefore \angle DAC=\angle DAB=30^{\circ}$, $AD// CH$. $\therefore \angle HCN=\angle CAD=\angle BAM=30^{\circ}$. $\because AM=CN$, $AB=BC=CH$, $\therefore \triangle ABM\cong \triangle CHN$. $\therefore BM=HN$. $\because BN+HN\geqslant BH$, $\therefore$ 当 $B$, $N$, $H$ 三点共线时, $BM+BN=NH+BN$ 的值最小. 如图②, 当 $B$, $N$, $H$ 三点共线时, $\because \triangle ABM\cong \triangle CHN$, $\therefore$ 易得 $\angle ABM=\angle CHB=\angle CBH=45^{\circ}$. $\because \angle ABD=60^{\circ}$, $\therefore \angle DBM=\angle ABD-\angle ABM=60^{\circ}-45^{\circ}=15^{\circ}$. $\therefore \angle MBN=\angle CBH-\angle DBM=45^{\circ}-15^{\circ}=30^{\circ}$. $\therefore$ 当 $BM+BN$ 的值最小时, $\angle MBN=30^{\circ}$.


$30^{\circ}$ 解析: 如图①, 过点 $C$ 作 $CH\perp BC$, 使得 $CH=BC$, 连接 $NH$, $BH$. $\because \triangle ABC$ 是等边三角形, $AD\perp BC$, $CH\perp BC$, $\therefore \angle DAC=\angle DAB=30^{\circ}$, $AD// CH$. $\therefore \angle HCN=\angle CAD=\angle BAM=30^{\circ}$. $\because AM=CN$, $AB=BC=CH$, $\therefore \triangle ABM\cong \triangle CHN$. $\therefore BM=HN$. $\because BN+HN\geqslant BH$, $\therefore$ 当 $B$, $N$, $H$ 三点共线时, $BM+BN=NH+BN$ 的值最小. 如图②, 当 $B$, $N$, $H$ 三点共线时, $\because \triangle ABM\cong \triangle CHN$, $\therefore$ 易得 $\angle ABM=\angle CHB=\angle CBH=45^{\circ}$. $\because \angle ABD=60^{\circ}$, $\therefore \angle DBM=\angle ABD-\angle ABM=60^{\circ}-45^{\circ}=15^{\circ}$. $\therefore \angle MBN=\angle CBH-\angle DBM=45^{\circ}-15^{\circ}=30^{\circ}$. $\therefore$ 当 $BM+BN$ 的值最小时, $\angle MBN=30^{\circ}$.


8. 如图,在△ABC中,点D,E在边AB上,且分别在AC,BC的垂直平分线上。
(1)若△CDE的周长为4,求AB的长。
(2)若∠ACB=100°,求∠DCE的度数。
(3)若∠ACB=x(90°<x<180°),求∠DCE的度数。
[img]
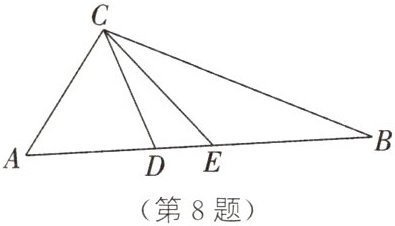
(1)若△CDE的周长为4,求AB的长。
(2)若∠ACB=100°,求∠DCE的度数。
(3)若∠ACB=x(90°<x<180°),求∠DCE的度数。
[img]

答案:
(1) $\because$ 点 $D$, $E$ 分别在 $AC$, $BC$ 的垂直平分线上, $\therefore DC=DA$, $EC=EB$. $\because \triangle CDE$ 的周长 $=DC+DE+EC=4$, $\therefore DA+DE+EB=4$, 即 $AB$ 的长为 $4$.
(2) $\because \angle ACB=100^{\circ}$, $\therefore \angle A+\angle B=80^{\circ}$. $\because DC=DA$, $\therefore \angle DCA=\angle A$. $\because EC=EB$, $\therefore \angle ECB=\angle B$. $\therefore \angle DCA+\angle ECB=80^{\circ}$. $\therefore \angle DCE=100^{\circ}-80^{\circ}=20^{\circ}$.
(3) $\because \angle ACB=x$, $\therefore \angle A+\angle B=180^{\circ}-x$. $\because DC=DA$, $\therefore \angle DCA=\angle A$. $\because EC=EB$, $\therefore \angle ECB=\angle B$. $\therefore \angle DCA+\angle ECB=180^{\circ}-x$. $\therefore \angle DCE=x-(180^{\circ}-x)=2x-180^{\circ}$.
(1) $\because$ 点 $D$, $E$ 分别在 $AC$, $BC$ 的垂直平分线上, $\therefore DC=DA$, $EC=EB$. $\because \triangle CDE$ 的周长 $=DC+DE+EC=4$, $\therefore DA+DE+EB=4$, 即 $AB$ 的长为 $4$.
(2) $\because \angle ACB=100^{\circ}$, $\therefore \angle A+\angle B=80^{\circ}$. $\because DC=DA$, $\therefore \angle DCA=\angle A$. $\because EC=EB$, $\therefore \angle ECB=\angle B$. $\therefore \angle DCA+\angle ECB=80^{\circ}$. $\therefore \angle DCE=100^{\circ}-80^{\circ}=20^{\circ}$.
(3) $\because \angle ACB=x$, $\therefore \angle A+\angle B=180^{\circ}-x$. $\because DC=DA$, $\therefore \angle DCA=\angle A$. $\because EC=EB$, $\therefore \angle ECB=\angle B$. $\therefore \angle DCA+\angle ECB=180^{\circ}-x$. $\therefore \angle DCE=x-(180^{\circ}-x)=2x-180^{\circ}$.
查看更多完整答案,请扫码查看


