《2025年拔尖特训八年级数学上册人教版》

1. 新考向·地方文化(2024·扬州)“致中和，天地位焉，万物育焉”，对称之美随处可见.下列图形中，是轴对称图形的为(C)

答案： C

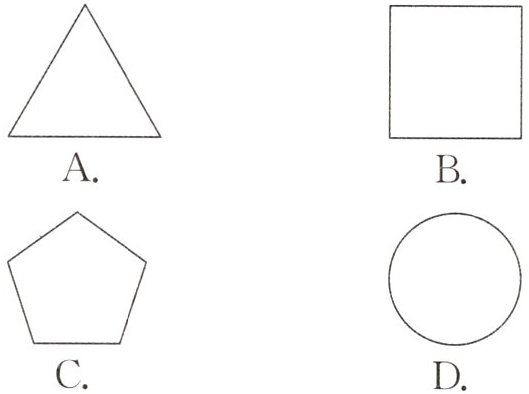
2. 下列图形中，对称轴的条数最多的是(D)

答案： D

3. 新考向·传统文化(2024·甘肃)围棋起源于我国，古代称为“弈”.如图所示为两名同学的部分对弈图，点A，B，C，D位于棋盘的格点上，现轮到白方落子，观察棋盘，白方如果落子于点A的位置，那么所得的对弈图是轴对称图形(填写A，B，C，D中的一处即可).

答案： A(或C)

4. 如图，六边形ABCDEF是轴对称图形，CF所在的直线是它的对称轴.如果$∠AFC+∠DCF=150^{\circ }$，那么$∠AFE+∠BCD=$$300^{\circ}$.

答案： $300^{\circ}$

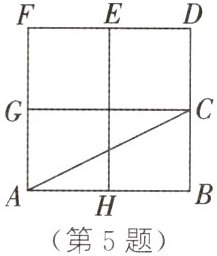
5. (2024·河池凤山期末)如图，在$2×2$的方格纸中，有一个以格点为顶点的$△ABC$，则与$△ABC$成轴对称且以格点为顶点的三角形共有( )

A. 3个
B. 4个
C. 5个
D. 6个

答案：
C 解析:如图,与$\triangle ABC$成轴对称且以格点为顶点的三角形有$\triangle BAG,\triangle FDC,\triangle AFE,\triangle DBH,\triangle GCB$,共5个.
　　　　

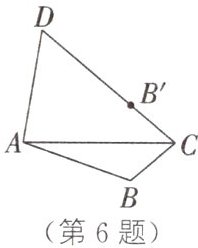
6. 如图，在四边形ABCD中，$AB=AD$，点B关于AC的对称点$B'$恰好落在CD上.若$∠BAD=100^{\circ }$，则$∠ACB$的度数为( )

A. $40^{\circ }$
B. $45^{\circ }$
C. $60^{\circ }$
D. $80^{\circ }$

答案：
A 解析:如图,连接$AB',BB'$,过点A作$AE\perp CD$于点E.$\because$点B关于AC的对称点$B'$恰好落在CD上,$\therefore$易得$AB = AB',\angle BAC=\angle B'AC.\because AB = AD,\therefore AD = AB'$.又$\because AE\perp CD,\therefore$易得$\angle DAE=\angle B'AE.\therefore$易得$\angle CAE=\frac{1}{2}\angle BAD = 50^{\circ}$.又$\because\angle AEC = 90^{\circ},\therefore$易得$\angle ACB=\angle ACB' = 90^{\circ}-50^{\circ}=40^{\circ}$.
　　　　

7. 如图，直线AB，CD相交于点O，P为这两条直线外一点，连接OP，点P关于直线AB，CD的对称点分别是$P_{1}$，$P_{2}$.若$OP=4$，则点$P_{1}$，$P_{2}$之间的距离可能是(B)
A. 0
B. 7
C. 9
D. 10

答案： B 解析:连接$OP_1,OP_2,P_1P_2$.$\because$点P关于直线AB,CD的对称点分别是$P_1,P_2,\therefore$易得$OP_1 = OP = 4,OP_2 = OP = 4.\because OP_1 - OP_2\lt P_1P_2\lt OP_1 + OP_2,\therefore 0\lt P_1P_2\lt 8.\therefore$点$P_1,P_2$之间的距离可能是7.

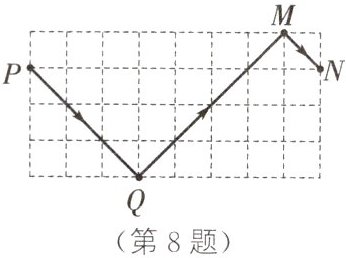
8. 如图，弹性小球从点P出发，沿图中所示的方向运动，每当小球碰到长方形的边时反弹，反弹时反射角等于入射角.记小球第1次碰到长方形的边时的点为Q，第2次碰到长方形的边时的点为M，第3次碰到长方形的边时的点为N……以此类推，第2024次碰到长方形的边时的点为图中的( )

A. P
B. Q
C. M
D. N

答案：
C 解析:如图,易得小球每经过6次反弹为一个循环.$\because 2024\div 6 = 337$(个)……2(次),$\therefore$第2024次碰到长方形的边时的点为图中的M.