《2025年拔尖特训八年级数学上册人教版》

1. 下列图形中，不一定全等的是 （C）
A. 两个半径相等的圆
B. 两个边长相等的正方形
C. 两个面积相等的矩形
D. 两个直角边相等的等腰直角三角形

答案： C

2. 如图，$\triangle ABC$与$\triangle DEF$全等，点$A$，$B$，$C$的对应点分别为$D$，$E$，$F$，且点$E$在$AC$上，$B$，$F$，$C$，$D$四点共线. 若$\angle A=40^{\circ}$，$\angle EFD=75^{\circ}$，则$\angle B=$65$^{\circ}$.

答案： 65

3. 如图，在$\triangle ABC$中，$D$，$E$分别是边$AC$，$BC$上的点. 若$\triangle ADB≌\triangle EDB≌\triangle EDC$，则$\angle ADB$的度数为$60^{\circ}$.

答案： $60^{\circ}$

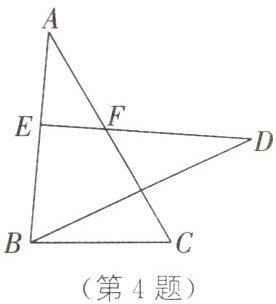
4. （2023·宜春期末）如图，$\triangle ABC≌\triangle DEB$，点$E$在边$AB$上，$DE$与$AC$相交于点$F$.
（1）若$AE=2$，$BC=3$，求线段$DE$的长.
（2）若$\angle C=50^{\circ}$，$\angle D=35^{\circ}$，求$\angle AFD$的度数.

答案：
(1) $\because \triangle ABC \cong \triangle DEB$，
$\therefore BC = EB = 3$，$AB = DE$。
$\because AB = AE + EB = 2 + 3 = 5$，
$\therefore DE = AB = 5$。
(2) $\because \triangle ABC \cong \triangle DEB$，
$\therefore \angle A = \angle D = 35^{\circ}$，$\angle DBE = \angle C = 50^{\circ}$。
$\because \angle AFD = \angle A + \angle AEF$，$\angle AEF = \angle D + \angle DBE$，
$\therefore \angle AFD = \angle A + \angle D + \angle DBE = 35^{\circ} + 35^{\circ} + 50^{\circ} = 120^{\circ}$。

5. 如图，$\triangle ABD≌\triangle EBC$，$AB=12$，$BC=5$，$A$，$B$，$C$三点共线. 有下列结论：①$CD\perp AE$；②$AD\perp CE$；③$ED=8$；④$\angle EAD=\angle ECD$. 其中，正确的是 （B）
A. ①②
B. ①②④
C. ②④
D. ②③④

答案： B

6. （2024·深圳福田期中）如图，在$4×4$的正方形网格中，$\angle 1+\angle 2+\angle 3+\angle 4+\angle 5+\angle 6+\angle 7$的度数为 （B）

A. $300^{\circ}$
B. $315^{\circ}$
C. $320^{\circ}$
D. $325^{\circ}$

答案： B

7. （2023·宜春期末）如图，$\triangle AOB≌\triangle ADC$，$\angle O=\angle D=90^{\circ}$，记$\angle OAD=\alpha$，$\angle ABO=\beta$. 当$BC// OA$时，$\alpha$与$\beta$之间的数量关系为 （B）

A. $\alpha=\beta$
B. $\alpha=2\beta$
C. $\alpha+\beta=90^{\circ}$
D. $\alpha+2\beta=180^{\circ}$

答案： B

8. 三个全等的三角形按如图所示的方式摆放，则$\angle 1+\angle 2+\angle 3$的度数为$180^{\circ}$.

答案： $180^{\circ}$

9. 如图，$N$，$C$，$A$三点在同一条直线上，$N$，$B$，$M$三点在同一条直线上. 在$\triangle ABC$中，$\angle A:\angle ABC:\angle ACB=3:5:10$，$\triangle MNC≌\triangle ABC$，则$\angle BCM$的度数为______$20^{\circ}$.

答案： $20^{\circ}$