《2025年拔尖特训八年级数学上册人教版》

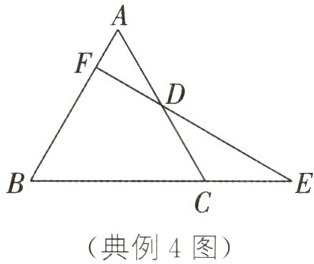
典例4 如图，△ABC是等边三角形，延长BC到点E，使CE=1/2BC，D是边AC的中点，连接ED并延长，交AB于点F。
(1)若AF=3，求AD的长。
(2)求证：DE=2DF。

答案：
(1) $\because \triangle ABC$ 是等边三角形, $\therefore AC=BC$, $\angle A=\angle ACB=60^{\circ}$. $\because D$ 是边 $AC$ 的中点, $\therefore CD=AD=\frac{1}{2}AC$. $\because CE=\frac{1}{2}BC$, $\therefore CE=CD$. $\therefore \angle E=\angle CDE$. $\because \angle ACB=\angle E+\angle CDE$, $\therefore \angle E=\angle CDE=30^{\circ}$. $\therefore \angle ADF=\angle CDE=30^{\circ}$. $\because \angle A=60^{\circ}$, $\therefore \angle AFD=180^{\circ}-\angle A-\angle ADF=90^{\circ}$. $\because AF=3$, $\therefore AD=2AF=6$.
(2) 连接 $BD$. $\because \triangle ABC$ 是等边三角形, $D$ 是边 $AC$ 的中点, $\therefore BD$ 平分 $\angle ABC$, $\angle ABC=60^{\circ}$. $\therefore \angle DBC=\angle ABD=\frac{1}{2}\angle ABC=30^{\circ}$. $\because \angle BFD=180^{\circ}-\angle AFD=90^{\circ}$, $\therefore BD=2DF$. $\because \angle DBC=\angle E=30^{\circ}$, $\therefore BD=DE$. $\therefore DE=2DF$.

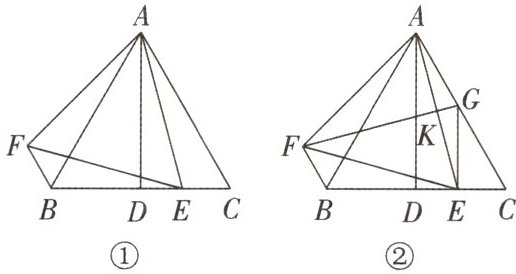
[变式] 如图①，△ABC是等边三角形，D为BC的中点，连接AD，AE平分∠DAC，交BC于点E，点F在△ABC外，连接FE，BF，AF，且BF//AC，∠AFB=∠AEC。
(1)求∠FAE的度数。
(2)如图②，G是AC上一点，连接EG，GF，GF与AE交于点K。若AK=EK，求证：CG=2CE。

答案：
(1) $\because \triangle ABC$ 是等边三角形, $\therefore \angle C=\angle BAC=60^{\circ}$, $AB=AC$. $\because BF// AC$, $\therefore \angle ABF=\angle BAC=60^{\circ}$. $\therefore \angle ABF=\angle C=60^{\circ}$. 在 $\triangle ABF$ 和 $\triangle ACE$ 中, $\left\{\begin{array}{l} \angle AFB=\angle AEC,\\ \angle ABF=\angle C,\\ AB=AC,\end{array}\right.$ $\therefore \triangle ABF\cong \triangle ACE$. $\therefore \angle BAF=\angle CAE$, $AF=AE$. $\therefore \angle FAE=\angle BAF+\angle BAE=\angle CAE+\angle BAE=\angle BAC=60^{\circ}$.
(2) 由
(1), 可知 $AF=AE$, $\angle FAE=60^{\circ}$. $\therefore \triangle AFE$ 是等边三角形. $\therefore \angle AFE=60^{\circ}$, $AF=EF$. $\because AK=EK$, $\therefore \angle AFG=\angle EFG=30^{\circ}$, $FK\perp AE$. 在 $\triangle AFG$ 和 $\triangle EFG$ 中, $\left\{\begin{array}{l} AF=EF,\\ \angle AFG=\angle EFG,\\ FG=FG,\end{array}\right.$ $\therefore \triangle AFG\cong \triangle EFG$. $\therefore \angle AGF=\angle EGF$. $\because \triangle ABC$ 是等边三角形, $D$ 为 $BC$ 的中点, $\therefore \angle DAC=\frac{1}{2}\angle BAC=30^{\circ}$. $\because AE$ 平分 $\angle DAC$, $\therefore \angle CAE=\frac{1}{2}\angle DAC=15^{\circ}$. $\because FK\perp AE$, $\therefore \angle AGF=90^{\circ}-\angle CAE=90^{\circ}-15^{\circ}=75^{\circ}$. $\therefore \angle AGF=\angle EGF=75^{\circ}$. $\therefore \angle CGE=180^{\circ}-(\angle AGF+\angle EGF)=30^{\circ}$. 又 $\because \angle C=60^{\circ}$, $\therefore \angle CEG=180^{\circ}-\angle C-\angle CGE=90^{\circ}$. 在 $Rt\triangle CEG$ 中, $\angle CGE=30^{\circ}$, $\therefore CG=2CE$.

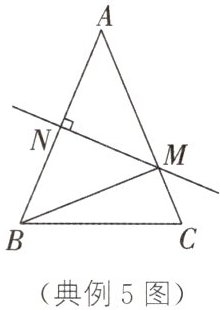
典例5 (2025·盐城射阳段考)如图，在△ABC中，AB=AC=8cm，AB的垂直平分线交AB于点N，交AC于点M，连接MB，△MBC的周长是14cm。
(1)求BC的长。
(2)在直线MN上是否存在点P，使PB+CP的值最小？若存在，直接写出PB+CP的最小值；若不存在，请说明理由。

答案：
(1) $\because MN$ 垂直平分 $AB$, $\therefore MB=MA$. 又 $\because \triangle MBC$ 的周长是 $14cm$, $\therefore BM+CM+BC=AM+CM+BC=AC+BC=14cm$. $\because AB=AC=8cm$, $\therefore BC=6cm$.
(2) 存在. 当点 $P$ 与点 $M$ 重合时, $PB+CP$ 的值最小, 最小值是 $8cm$.

如图，在四边形ABCD中，∠ABC=60°，BD平分∠ABC，∠BCD＞∠CBD，BC=24，P，Q分别是BD，BC上的动点，则当CP+PQ取得最小值时，BQ的长是12。

答案： 12