《2025年拔尖特训八年级数学上册人教版》

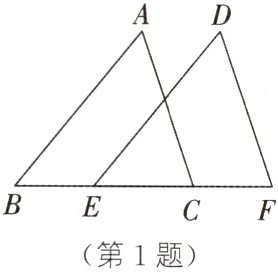
1. (2023·衢州)如图,在△ABC和△DEF中,点B,E,C,F在同一条直线上.有下列四个条件:①AB=DE;②AC=DF;③BE=CF;④∠ABC=∠DEF.
(1)请选择其中的三个条件,使得△ABC≌△DEF(写出一种情况即可).
(2)在(1)的条件下,求证:△ABC≌△DEF.

答案：
(1) 选择不唯一，如选择的三个条件是①②③.
(2)
∵ $ BE = CF $，
∴ $ BE + EC = CF + EC $，即 $ BC = EF $.
在 $ \triangle ABC $ 和 $ \triangle DEF $ 中，$ \left\{ \begin{array} { l } { AB = DE }, \\ { BC = EF }, \\ { AC = DF }, \end{array} \right. $
∴ $ \triangle ABC \cong \triangle DEF ( SSS ) $.

2. (2025·天津西青期中)如图,AC=AE,∠C=∠E,∠1=∠2.求证:△ABC≌△ADE.

答案：
∵ $ \angle 1 = \angle 2 $，
∴ $ \angle 1 + \angle EAC = \angle 2 + \angle EAC $.
∴ $ \angle BAC = \angle DAE $.
在 $ \triangle ABC $ 和 $ \triangle ADE $ 中，
$ \left\{ \begin{array} { l } { \angle BAC = \angle DAE }, \\ { AC = AE }, \\ { \angle C = \angle E }, \end{array} \right. $
∴ $ \triangle ABC \cong \triangle ADE ( ASA ) $.

3. 如图,AB⊥AC于点A,AB=AC,AD⊥AE于点A,AD=AE.若∠D=35°,∠B=15°,则∠CAE的度数为40°.

答案： $ 40 ^ { \circ } $

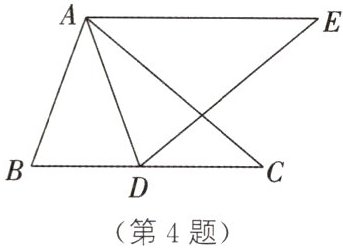
4. 如图,AE//BC,AB=AD,∠BAD=∠EAC=∠E.
(1)求证:△ABC≌△ADE.
(2)若∠BAE=110°,求∠E的度数.

答案：
(1)
∵ $ \angle BAD = \angle EAC $，
∴ $ \angle BAD + \angle CAD = \angle EAC + \angle CAD $，即 $ \angle BAC = \angle DAE $.
∵ $ AE // BC $，
∴ $ \angle EAC = \angle C $.
∵ $ \angle EAC = \angle E $，
∴ $ \angle C = \angle E $.
在 $ \triangle ABC $ 和 $ \triangle ADE $ 中，
$ \left\{ \begin{array} { l } { \angle C = \angle E }, \\ { \angle BAC = \angle DAE }, \\ { AB = AD }, \end{array} \right. $
∴ $ \triangle ABC \cong \triangle ADE ( AAS ) $.
(2)
∵ $ \angle BAE = 110 ^ { \circ }, AE // BC $，
∴ $ \angle B = 180 ^ { \circ } - \angle BAE = 70 ^ { \circ } $.
∵ $ AB = AD $，
∴ $ \angle B = \angle ADB = 70 ^ { \circ } $.
∴ $ \angle BAD = 180 ^ { \circ } - \angle B - \angle ADB = 40 ^ { \circ } $.
∴ $ \angle E = \angle BAD = 40 ^ { \circ } $.

5. 如图,点C,E,F,B在同一条直线上,点A,D在BC的异侧,AB//CD,AE=DF,∠A=∠D.
(1)求证:AB=DC.
(2)若AB=CF,∠B=40°,求∠D的度数.

答案：
(1)
∵ $ AB // CD $，
∴ $ \angle B = \angle C $.
在 $ \triangle ABE $ 和 $ \triangle DCF $ 中，
$ \left\{ \begin{array} { l } { \angle B = \angle C }, \\ { \angle A = \angle D }, \\ { AE = DF }, \end{array} \right. $
∴ $ \triangle ABE \cong \triangle DCF ( AAS ) $.
∴ $ AB = DC $.
(2)
∵ $ \angle B = 40 ^ { \circ }, \angle B = \angle C $，
∴ $ \angle C = 40 ^ { \circ } $.
∵ $ \triangle ABE \cong \triangle DCF $，
∴ $ AB = DC $.
∵ $ AB = CF $，
∴ $ CD = CF $.
过点 $ C $ 作 $ CM \perp DF $ 于点 $ M $，
易得 $ Rt \triangle CMD \cong Rt \triangle CMF ( HL ) $，
∴ $ \angle D = \angle CFD = \frac { 1 } { 2 } ( 180 ^ { \circ } - \angle DCF ) = \frac { 1 } { 2 } \times ( 180 ^ { \circ } - 40 ^ { \circ } ) = 70 ^ { \circ } $.