《2025年拔尖特训八年级数学上册人教版》

1. 如图,在$\triangle ABC$中,$AB$的垂直平分线$DE$交$AC$于点$D$,垂足为$E$,连接$BD$.如果$\triangle DBC$的周长为$10\mathrm{c}\mathrm{m}$,$BC=4\mathrm{c}\mathrm{m}$,那么$AC$的长为(B)
A. $5\mathrm{c}\mathrm{m}$
B. $6\mathrm{c}\mathrm{m}$
C. $7\mathrm{c}\mathrm{m}$
D. $9\mathrm{c}\mathrm{m}$

答案： B

2. 下列命题中,逆命题是真命题的为(D)
A. 如果两个直角三角形全等,那么它们的斜边相等
B. 如果两个数的商为$-1$,那么这两个数互为相反数
C. 如果$a = b$,那么$a^{2} = b^{2}$
D. 如果一个三角形是等腰三角形,那么这个三角形两腰上的高相等

答案： D

3. 如图,在$\mathrm{R}\mathrm{t}\triangle ABC$中,$\angle ABC = 90^{\circ}$,$ED$是$AC$的垂直平分线,交$AC$于点$D$,交$BC$于点$E$,连接$AE$.若$\angle BAE = 10^{\circ}$,则$\angle C$的度数为$40^{\circ}$.

答案： $40^{\circ}$ 解析：$\because ED$是$AC$的垂直平分线，$\therefore AE = EC$。$\therefore \angle EAC=\angle C$。$\because \angle ABC = 90^{\circ}$，$\angle BAE = 10^{\circ}$，$\therefore \angle EAC+\angle C=\angle AEB = 180^{\circ}-\angle BAE-\angle ABC = 80^{\circ}$。$\therefore \angle EAC=\angle C = 40^{\circ}$。

4. $^{\star}$如图,在$\mathrm{R}\mathrm{t}\triangle ABC$中,$\angle C = 90^{\circ}$,$AB = 2AC$,$AD$平分$\angle BAC$,交$BC$于点$D$.求证:点$D$在线段$AB$的垂直平分线上.

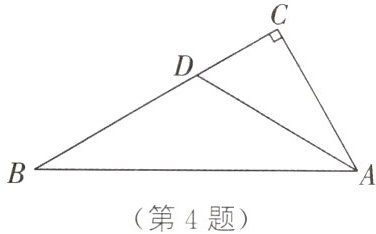
答案： 过点$D$作$DE\perp AB$于点$E$，则$\angle AED = 90^{\circ}$。$\because \angle C = 90^{\circ}$，$\therefore \angle AED=\angle C = 90^{\circ}$。$\because AD$平分$\angle BAC$，$\therefore \angle EAD=\angle CAD$。在$\triangle AED$和$\triangle ACD$中，$\because \angle AED=\angle C$，$\angle EAD=\angle CAD$，$AD = AD$，$\therefore \triangle AED\cong\triangle ACD$。$\therefore AE = AC$。$\because AB = 2AC$，$\therefore AB = 2AE$。$\therefore BE = AE$。又$\because DE\perp AB$，$\therefore DE$所在的直线是线段$AB$的垂直平分线。$\therefore$点$D$在线段$AB$的垂直平分线上。
方法归纳：证明一条直线是某条线段的垂直平分线的条件：（1）存在两点：直线上有两个不同的点；（2）到两端点的距离相等：两点到线段两个端点的距离分别相等。根据两点确定一条直线，推导出这两个点所在的直线就是这条线段的垂直平分线。

5. 如图,在$\triangle ABC$中,$AB$,$AC$的垂直平分线$l_{1}$,$l_{2}$相交于点$O$,连接$OB$,$OC$.若$\angle BAC = 78^{\circ}$,则$\angle OBC$的度数为( )

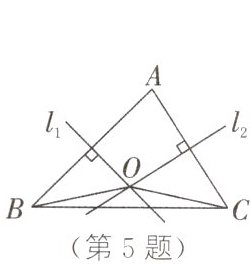
A. $6^{\circ}$
B. $8^{\circ}$
C. $12^{\circ}$
D. $16^{\circ}$

答案：
C 解析：如图，连接$AO$。$\because l_{1}$垂直平分$AB$，$l_{2}$垂直平分$AC$，$\therefore AO = BO$，$AO = CO$。$\therefore \angle OBA=\angle OAB$，$\angle OCA=\angle OAC$。$\because \angle OAB+\angle OAC=\angle BAC = 78^{\circ}$，$\therefore \angle OBA+\angle OCA=\angle OAB+\angle OAC = 78^{\circ}$。$\because \angle ABC+\angle ACB = 180^{\circ}-\angle BAC = 180^{\circ}-78^{\circ}=102^{\circ}$，$\therefore \angle OBC+\angle OCB=\angle ABC-\angle OBA+\angle ACB-\angle OCA = 102^{\circ}-78^{\circ}=24^{\circ}$。$\because AO = BO$，$AO = CO$，$\therefore BO = CO$。$\therefore \angle OBC=\angle OCB = 12^{\circ}$。

6. 如图,线段$AB$,$DE$的垂直平分线交于点$C$,且$\angle ABC = \angle EDC = 72^{\circ}$,$\angle AEB = 92^{\circ}$,则$\angle EBD$的度数为( )

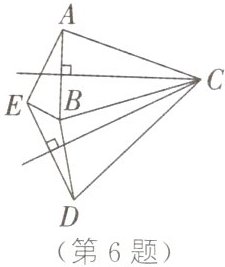
A. $168^{\circ}$
B. $158^{\circ}$
C. $128^{\circ}$
D. $118^{\circ}$

答案：
C 解析：如图，连接$CE$。$\because$线段$AB$，$DE$的垂直平分线交于点$C$，$\therefore CA = CB$，$CE = CD$。$\because$易得$\angle ABC=\angle EDC = 72^{\circ}=\angle DEC=\angle BAC$，$\therefore \angle ACB=\angle ECD = 36^{\circ}$。$\therefore$易得$\angle ACE=\angle BCD$。在$\triangle ACE$和$\triangle BCD$中，$\left\{\begin{array}{l}CA = CB,\\ \angle ACE=\angle BCD,\\ CE = CD,\end{array}\right.$ $\therefore \triangle ACE\cong\triangle BCD$。$\therefore \angle AEC=\angle BDC$。设$\angle AEC=\angle BDC=\alpha$，则$\angle BDE=\angle EDC-\angle BDC = 72^{\circ}-\alpha$，$\angle CEB=\angle AEB-\angle AEC = 92^{\circ}-\alpha$。$\therefore \angle BED=\angle DEC-\angle CEB = 72^{\circ}-(92^{\circ}-\alpha)=\alpha - 20^{\circ}$。$\therefore$在$\triangle BDE$中，$\angle EBD = 180^{\circ}-\angle BDE-\angle BED = 180^{\circ}-(72^{\circ}-\alpha)-(\alpha - 20^{\circ}) = 128^{\circ}$。

7. 如图,在$\triangle ABC$中,$BC$的垂直平分线$DE$交$AC$于点$D$,交$BC$于点$E$,连接$BD$.若$AD = 3$,$AC = 5$,设$AB$的长为$m$,则$m$的取值范围是$1\lt m\lt5$.

答案： $1\lt m\lt5$ 解析：$\because AD = 3$，$AC = 5$，$DE$垂直平分$BC$，$\therefore BD = CD = 5 - 3 = 2$。$\because AD - BD\lt AB\lt AD + BD$，$\therefore 3 - 2\lt m\lt3 + 2$，即$1\lt m\lt5$。

8. 如图,在四边形$ABCD$中,$\angle B = \angle C$,$AB + CD = BC$,$M$为$AD$的中点,$MN\perp AD$交$BC$于点$N$,连接$AN$,$DN$,则$\angle ANM$与$\angle B$的数量关系是______$\angle ANM=\frac{1}{2}\angle B$.

答案： $\angle ANM=\frac{1}{2}\angle B$ 解析：在线段$BC$上取一点$N'$，使得$BN' = CD$。连接$AN'$，$DN'$，$MN'$。$\because AB + CD = BC$，$CN' + BN' = BC$，$\therefore CN' = AB$。$\because \angle B=\angle C$，$\therefore \triangle ABN'\cong\triangle N'CD$。$\therefore AN' = N'D$，$\angle BAN'=\angle CN'D$。$\because M$为$AD$的中点，$\therefore AM = MD$。又$\because MN' = MN'$，$\therefore \triangle AMN'\cong\triangle DMN'$。$\therefore \angle AMN'=\angle DMN'$。$\because \angle AMN'+\angle DMN' = 180^{\circ}$，$\therefore \angle AMN'=\angle DMN' = 90^{\circ}$。$\therefore MN'\perp AD$。$\because MN\perp AD$，$\therefore$点$N$与点$N'$重合。$\because \angle ANC=\angle AND+\angle DNC=\angle B+\angle BAN$，$\therefore \angle AND=\angle B$。$\because NA = ND$，$NM\perp AD$，易证$Rt\triangle AMN\cong Rt\triangle DMN$，$\therefore \angle ANM=\angle DNM$。$\therefore \angle AND = 2\angle ANM$。$\therefore \angle ANM=\frac{1}{2}\angle B$。

9. 如图,在$\triangle ABC$中,$E$是边$BC$上的一点,连接$AE$,$BD$垂直平分线段$AE$,垂足为$F$,交$AC$于点$D$,连接$DE$.
(1) 若$AB = 6$,$\triangle DEC$的周长为$7$,则$\triangle ABC$的周长为______19.
(2) 若$\angle ABD = 15^{\circ}$,$\angle C = 45^{\circ}$,则$\angle CED$的度数为______75°.

答案： （1）19 解析：$\because BD$垂直平分线段$AE$，$\therefore BA = BE$，$DA = DE$。又$\because AB = 6$，$\therefore BE = 6$。$\because \triangle DEC$的周长为$7$，即$DE + CE + CD = 7$，$\therefore AC + EC = AD + DC + EC = DE + DC + EC = 7$。$\therefore \triangle ABC$的周长为$AB + BC + AC = AB + BE + EC + AC = 6 + 6 + 7 = 19$。
（2）$75^{\circ}$ 解析：$\because BD$垂直平分线段$AE$，$\therefore AB = BE$，$DA = DE$，$\angle AFB = 90^{\circ}$。$\therefore \angle BAE=\angle BEA$。$\because \angle ABD = 15^{\circ}$，$\therefore \angle BEA=\angle BAE = 180^{\circ}-90^{\circ}-15^{\circ}=75^{\circ}$。又$\because \angle C = 45^{\circ}$，$\therefore \angle CAE = 75^{\circ}-45^{\circ}=30^{\circ}$。$\because DA = DE$，$\therefore \angle DEA=\angle DAE = 30^{\circ}$。$\therefore \angle CED = 180^{\circ}-75^{\circ}-30^{\circ}=75^{\circ}$。