《2025年拔尖特训八年级数学上册人教版》

1. 把12 cm长的铁丝截成三段，首尾顺次相接，围成三边长均不相等的三角形，且使三边长均为整数，截法有（A）
A. 一种
B. 两种
C. 三种
D. 四种

答案： 1. A

2. (2025·抚顺期中)在$Rt\triangle ABC$中，$\angle C=90^{\circ}$，$\angle A:\angle B=1:2$，则两个锐角的度数为（A）
A. $30^{\circ}$和$60^{\circ}$
B. $45^{\circ}$和$45^{\circ}$
C. $40^{\circ}$和$80^{\circ}$
D. 以上说法都不对

答案： 2. A

3. 如图，$AD$是$\angle BAC$的平分线，$\angle ADB=100^{\circ}$，$\angle DBC=25^{\circ}$，$\angle C=53^{\circ}$，则$\angle DBA$的度数为（）

A. $52^{\circ}$
B. $42^{\circ}$
C. $58^{\circ}$
D. $32^{\circ}$

答案：
3. C　解析:如图,连接$CD$并延长,交$AB$于点$E$.$\because \angle BDE$是$\triangle BCD$的外角,$\angle ADE$是$\triangle ACD$的外角,$\therefore \angle BDE = \angle DBC + \angle BCD$,$\angle ADE = \angle CAD + \angle ACD$.$\therefore \angle BDE + \angle ADE = \angle DBC + \angle BCD + \angle CAD + \angle ACD$,即$\angle ADB = \angle DBC + \angle CAD + \angle ACB$.$\therefore \angle CAD = \angle ADB - \angle DBC - \angle ACB = 100^{\circ} - 25^{\circ} - 53^{\circ} = 22^{\circ}$.$\because AD$是$\angle BAC$的平分线,$\therefore \angle BAD = \angle CAD = 22^{\circ}$.在$\triangle ABD$中,$\angle BAD = 22^{\circ}$,$\angle ADB = 100^{\circ}$,$\therefore \angle DBA = 180^{\circ} - \angle BAD - \angle ADB = 180^{\circ} - 22^{\circ} - 100^{\circ} = 58^{\circ}$.
　　　　

4. 如图，在$\triangle ABC$中，$AD$是$\triangle ABC$的角平分线，点$F$在射线$AD$上，$FE\perp BC$于点$E$，$\angle C=80^{\circ}$，$\angle B=36^{\circ}$，则$\angle F$的度数为$22^{\circ}$。

答案： 4.　$22^{\circ}$　解析:在$\triangle ABC$中,$\because \angle B = 36^{\circ}$,$\angle C = 80^{\circ}$,$\therefore \angle BAC = 180^{\circ} - \angle B - \angle C = 180^{\circ} - 36^{\circ} - 80^{\circ} = 64^{\circ}$.$\because AD$平分$\angle BAC$,$\therefore \angle BAD = \angle CAD = \frac{1}{2}\angle BAC = \frac{1}{2}×64^{\circ} = 32^{\circ}$.$\because FE \perp BC$,$\therefore \angle DEF = 90^{\circ}$.$\because \angle ADB$是$\triangle ACD$的外角,$\angle ADB$是$\triangle DEF$的外角,$\therefore \angle ADB = \angle CAD + \angle C = \angle F + \angle DEF$,即$32^{\circ} + 80^{\circ} = \angle F + 90^{\circ}$.$\therefore \angle F = 22^{\circ}$.

5. (2024·商丘睢阳期末)如图，在$Rt\triangle ABC$中，$\angle ACB=90^{\circ}$，点$D$在边$AB$上，将$\triangle CBD$沿$CD$折叠，使点$B$恰好落在边$AC$上的点$E$处。若$\angle A=25^{\circ}$，则$\angle CDE=$$70^{\circ}$。

答案： 5. $70^{\circ}$　解析:$\because$将$\triangle CBD$沿$CD$折叠,使点$B$恰好落在边$AC$上的点$E$处,$\angle ACB = 90^{\circ}$,$\therefore \angle BCD = \angle ECD = \frac{1}{2}\angle ACB = 45^{\circ}$,$\angle B = \angle CED$.$\because \angle A = 25^{\circ}$,$\therefore \angle B = 90^{\circ} - \angle A = 90^{\circ} - 25^{\circ} = 65^{\circ}$.$\therefore \angle CED = 65^{\circ}$.$\therefore \angle CDE = 180^{\circ} - \angle ECD - \angle CED = 180^{\circ} - 45^{\circ} - 65^{\circ} = 70^{\circ}$.

6. 已知$\triangle ABC$的两边长分别为3和7，第三边的长是关于$x$的方程$\frac{x+a}{2}=x+1$的解，则$a$的取值范围是$6 ＜ a ＜ 12$。

答案： 6. $6 ＜ a ＜ 12$

7. (2024·济南商河期末改编)如图，在$\triangle ABC$中，$BE$，$CE$，$CD$分别平分$\angle ABC$，$\angle ACB$，$\angle ACF$，$AB// CD$，有下列结论：①$\angle BDC=\angle BAC$；②$\angle BEC=90^{\circ}+\angle ABD$；③$\angle CAB=\angle CBA$。其中，正确的为②③(填序号)。

答案： 7. ②③　解析:$\because CD$平分$\angle ACF$,$\angle ACF = \angle ABC + \angle BAC$,$\therefore \angle ACD = \angle DCF = \frac{1}{2}\angle ACF = \frac{1}{2}\angle ABC + \frac{1}{2}\angle BAC$.$\because BE$平分$\angle ABC$,$\therefore \angle ABD = \angle CBD = \frac{1}{2}\angle ABC$.$\therefore \angle DCF = \angle DBC + \angle BDC = \frac{1}{2}\angle ABC + \angle BDC$.$\therefore \frac{1}{2}\angle BAC = \angle BDC$,即$\angle BAC = 2\angle BDC$.故①错误.$\because CE$平分$\angle ACB$,$\therefore \angle ACE = \frac{1}{2}\angle ACB$.$\because \angle ACB + \angle ACF = 180^{\circ}$,$\therefore \angle ACE + \angle ACD = 90^{\circ}$,即$\angle ECD = 90^{\circ}$.$\therefore \angle BEC = \angle ECD + \angle CDB = 90^{\circ} + \angle CDB$.$\because CD // AB$,$\therefore \angle CDB = \angle ABD$.$\therefore \angle BEC = 90^{\circ} + \angle ABD$.故②正确.$\because BD$平分$\angle CBA$,$\therefore \angle CBA = 2\angle ABD = 2\angle CDB$.$\because \angle BAC = 2\angle BDC$,$\therefore \angle CAB = \angle CBA$.故③正确.综上所述,正确的为②③.

8. (2025·商洛商南段考)已知$a$，$b$，$c$分别为$\triangle ABC$的三边长，且满足$a+b=3c-2$，$a-b=2c-6$。
(1)求$c$的取值范围。
(2)若$\triangle ABC$的周长为18，求$c$的值。

答案： 8.
(1)$\because a$,$b$,$c$分别为$\triangle ABC$的三边长,$a + b = 3c - 2$,$a - b = 2c - 6$,$\therefore \begin{cases}3c - 2 ＞ c\\|2c - 6| ＜ c\end{cases}$,即$\begin{cases}2c ＞ 2\\ - c ＜ 2c - 6 ＜ c\end{cases}$,解得$2 ＜ c ＜ 6$.
(2)$\because \triangle ABC$的周长为$18$,$a + b = 3c - 2$,$\therefore a + b + c = 4c - 2 = 18$,解得$c = 5$.

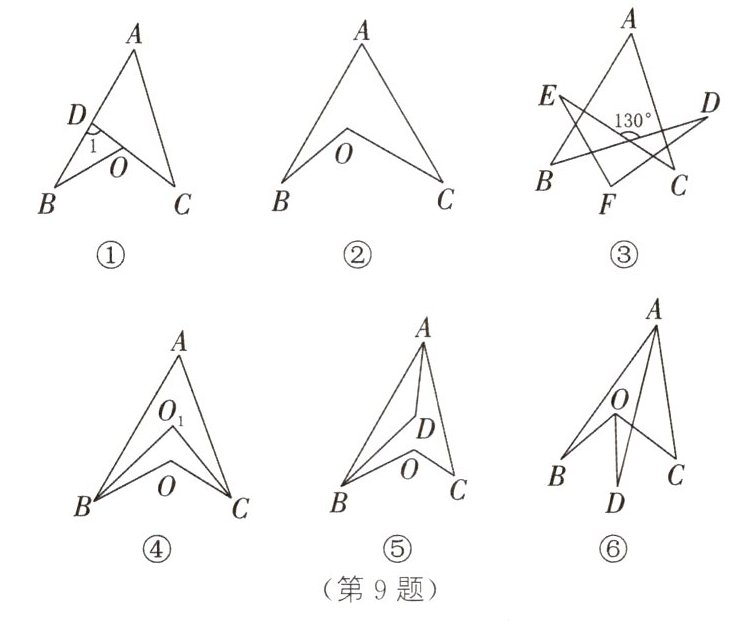
9. 【模型规律】如图①，延长$CO$交$AB$于点$D$，则$\angle BOC=\angle 1+\angle B=\angle A+\angle C+\angle B$。因为凹四边形答案讲解$ABOC$形如箭头，其四角具有“$\angle BOC=\angle A+\angle B+\angle C$”这个规律，所以我们把这个模型叫作“箭头四角形”。
【模型应用】(1)①如图②，$\angle A=60^{\circ}$，$\angle B=20^{\circ}$，$\angle C=30^{\circ}$，则$\angle BOC$的度数为$110^{\circ}$。
②如图③，$\angle A+\angle B+\angle C+\angle D+\angle E+\angle F$的度数为$260^{\circ}$。
(2)①如图④，$\angle ABO$，$\angle ACO$的平分线$BO_1$，$CO_1$交于点$O_1$。若$\angle BOC=120^{\circ}$，$\angle A=50^{\circ}$，则$\angle BO_1C$的度数为$85^{\circ}$。
②如图⑤，$\angle ABO$，$\angle BAC$的平分线$BD$，$AD$交于点$D$。若$\angle BOC=120^{\circ}$，$\angle C=44^{\circ}$，则$\angle ADB$的度数为$142^{\circ}$。
③如图⑥，$\angle BAC$，$\angle BOC$的平分线$AD$，$OD$交于点$D$，求$\angle B$，$\angle C$，$\angle D$之间的数量关系。

$\because$易得$\angle DOC + \angle D = \angle DAC + \angle C$,$\therefore \angle D = \angle DAC + \angle C - \angle DOC$.$\because AD$,$OD$分别是$\angle BAC$,$\angle BOC$的平分线,$\therefore \angle DAC = \frac{1}{2}\angle BAC$,$\angle DOC = \frac{1}{2}\angle BOC = \frac{1}{2}(\angle BAC + \angle B + \angle C)$.$\therefore \angle D = \frac{1}{2}\angle BAC + \angle C - \frac{1}{2}(\angle BAC + \angle B + \angle C) = \frac{1}{2}\angle C - \frac{1}{2}\angle B = \frac{1}{2}(\angle C - \angle B)$

答案： 9.
(1)①$110^{\circ}$.②$260^{\circ}$.
(2)①$85^{\circ}$.②$142^{\circ}$.③$\because$易得$\angle DOC + \angle D = \angle DAC + \angle C$,$\therefore \angle D = \angle DAC + \angle C - \angle DOC$.$\because AD$,$OD$分别是$\angle BAC$,$\angle BOC$的平分线,$\therefore \angle DAC = \frac{1}{2}\angle BAC$,$\angle DOC = \frac{1}{2}\angle BOC = \frac{1}{2}(\angle BAC + \angle B + \angle C)$.$\therefore \angle D = \frac{1}{2}\angle BAC + \angle C - \frac{1}{2}(\angle BAC + \angle B + \angle C) = \frac{1}{2}\angle C - \frac{1}{2}\angle B = \frac{1}{2}(\angle C - \angle B)$.