《2025年拔尖特训八年级数学上册人教版》

9. 在$△ABC$中，将$∠B$，$∠C$按如图所示的方式折叠，使点B，C均落在边BC上的点G处，线段MN，EF为折痕.若$∠A=80^{\circ }$，则$∠MGE$的度数为____$80^{\circ}$.

答案： $80^{\circ}$

10. 如图，在$△ABC$中，$∠C=90^{\circ }$，点M，N分别在边AB，BC上，且点A，B关于直线MN对称，连接AN.
(1)若$∠CAN=α$，则$∠B$与α之间的数量关系为$\alpha + 2\angle B = 90^{\circ}$.
(2)若$BC=\frac {4}{3}AC$，$AB=\frac {5}{3}AC$，且$△ABC$的周长为24，求AC的长.$\because\triangle ABC$的周长为24,$\therefore AC + BC + AB = 24.\because BC=\frac{4}{3}AC,AB=\frac{5}{3}AC,\therefore AC+\frac{4}{3}AC+\frac{5}{3}AC = 24$,解得$AC = 6.\therefore AC$的长为6.

答案：
(1)$\alpha + 2\angle B = 90^{\circ}$. 解析:$\because\angle C = 90^{\circ},\therefore\angle CAB+\angle B = 90^{\circ}$,即$\alpha+\angle NAB+\angle B = 90^{\circ}.\because$点A,B关于直线MN对称,$\therefore$易得$\angle NAB=\angle B.\therefore\alpha + 2\angle B = 90^{\circ}$.
(2)$\because\triangle ABC$的周长为24,$\therefore AC + BC + AB = 24.\because BC=\frac{4}{3}AC,AB=\frac{5}{3}AC,\therefore AC+\frac{4}{3}AC+\frac{5}{3}AC = 24$,解得$AC = 6.\therefore AC$的长为6.

11. (2024·福建)小明用两个全等的等腰三角形设计了一个“蝴蝶”的平面图案，如图，其中$△OAB$与$△ODC$都是等腰三角形，且它们关于直线l对称，E，F分别是底边AB，CD的中点，$OE⊥OF$.下列推断错误的是(B)
A. $OB⊥OD$
B. $∠BOC=∠AOB$
C. $OE=OF$
D. $∠BOC+∠AOD=180^{\circ }$

答案： B 解析:$\because\triangle OAB$与$\triangle ODC$都是等腰三角形,且它们关于直线l对称,$\therefore\triangle OAB\cong\triangle ODC.\therefore\angle AOB=\angle COD.\because E,F$分别是底边AB,CD的中点,$\therefore$易得$\angle AOE=\angle BOE=\frac{1}{2}\angle AOB,\angle COF=\angle DOF=\frac{1}{2}\angle COD.\therefore\angle AOE=\angle BOE=\angle COF=\angle DOF.\because OE\perp OF,\therefore\angle BOE+\angle BOF = 90^{\circ}.\because\angle BOE=\angle DOF,\therefore\angle DOF+\angle BOF = 90^{\circ}.\therefore OB\perp OD$.故A正确.由已有条件无法证明$\angle BOC=\angle AOB$.故B错误.$\because\triangle OAB\cong\triangle ODC,\therefore OB = OC,\angle B=\angle C.\because\angle BOE=\angle COF,\therefore\triangle OBE\cong\triangle OCF.\therefore OE = OF$.故C正确.由选项A的分析知,$OB\perp OD,\therefore\angle BOC+\angle COD = 90^{\circ}$①.$\because OE\perp OF,\therefore\angle COF+\angle EOC = 90^{\circ}.\because\angle COF=\angle AOE,\therefore\angle AOE+\angle EOC = 90^{\circ}.\therefore OC\perp OA.\therefore\angle AOB+\angle BOC = 90^{\circ}$②.①+②,得$\angle BOC+\angle COD+\angle AOB+\angle BOC = 180^{\circ}$,即$\angle BOC+\angle AOD = 180^{\circ}$.

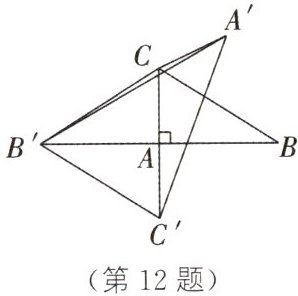
12. 如图，在$△ABC$中，$∠BAC=90^{\circ }$，点A关于BC的对称点为$A'$，点B关于AC的对称点为$B'$，点C关于AB的对称点为$C'$，连接$AB'$，$A'C$，$AC'$，$B'C$，$A'B'$，$B'C'$，$A'C'$.若$S_{△ABC}=1$，求$S_{△A'B'C'}$.

答案： 连接$A'A$交BC于点D,延长$A'A$交$B'C'$于点E.$\because$点A关于BC的对称点为$A',\therefore DA' = DA,AA'\perp BC.\because$点B关于AC的对称点为$B',\therefore BA = B'A,BB'\perp AC.\because$点C关于AB的对称点为$C',\therefore AC = AC',CC'\perp AB.\therefore$易得$\angle BAC=\angle B'AC' = 90^{\circ}$.在$\triangle ABC$和$\triangle AB'C'$中,$\left\{\begin{array}{l}AB = AB',\\\angle BAC=\angle B'AC',\\AC = AC',\end{array}\right.$$\therefore\triangle ABC\cong\triangle AB'C'.\therefore BC = B'C',\angle B=\angle AB'C',S_{\triangle ABC}=S_{\triangle AB'C'}.\therefore BC// B'C'.\because AA'\perp BC,\therefore$易得$AE\perp B'C',S_{\triangle ABC}=\frac{1}{2}BC\cdot AD.\therefore S_{\triangle AB'C'}=\frac{1}{2}B'C'\cdot AE.\therefore AD = AE.\therefore A'E = 3AD.\therefore S_{\triangle A'B'C'}=\frac{1}{2}B'C'\cdot A'E=\frac{1}{2}\times BC\cdot 3AD = 3S_{\triangle ABC}=3\times 1 = 3$.