第28页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
1. (2024·大连中山期末)下列尺规作图的语句正确的是 (
A. 连接BC,使$BC⊥AB$
B. 以点C为圆心,AB为半径作弧
C. 作直线$AB=3cm$
D. 连接AD,并且平分$∠BAC$
B
)A. 连接BC,使$BC⊥AB$
B. 以点C为圆心,AB为半径作弧
C. 作直线$AB=3cm$
D. 连接AD,并且平分$∠BAC$
答案:
B
2. 数学课上,老师提出一个问题:经过已知角一边上的点,作一个角等于已知角.如图,用直尺和圆规过$∠AOB$的边OB上一点C(如图①)作$∠DCB=∠AOB$(如图②).我们可以通过以下步骤作图(顺序已打乱):① 过点C,Q作射线CD;② 以点O为圆心,小于OC的长为半径作弧,分别交OA,OB于点N,M;③ 以点P为圆心,MN为半径作弧,交上一段弧于点Q;④ 以点C为圆心,OM为半径作弧,交OB于点P.下列排序正确的是 (
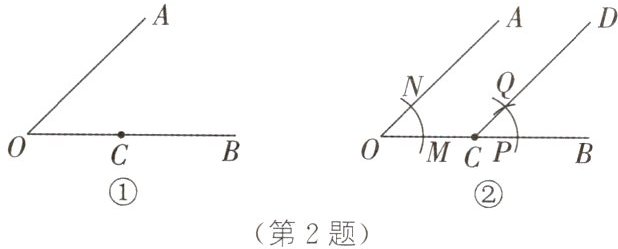
A. ①②③④
B. ④③①②
C. ③②④①
D. ②④③①
D
)
A. ①②③④
B. ④③①②
C. ③②④①
D. ②④③①
答案:
D
3. 有下列作图:① 用直尺和圆规作线段a等于已知线段;② 用直尺和圆规作一个角等于已知角;③ 用刻度尺和圆规作一条10 cm的线段;④ 用直尺和圆规作一个三角形.其中,属于尺规作图的是
①②④
(填序号).
答案:
①②④
4. 如图,已知$△ABC$.
(1)【实践与操作】利用直尺和圆规,在$△ABC$的边AC上方作$∠CAE=∠ACB$,在射线AE上截取$AD=BC$,连接CD(尺规作图,要求保留作图痕迹,不写作法).
(2)【应用与证明】求证:$CD// AB$.
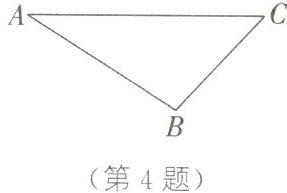
(1)【实践与操作】利用直尺和圆规,在$△ABC$的边AC上方作$∠CAE=∠ACB$,在射线AE上截取$AD=BC$,连接CD(尺规作图,要求保留作图痕迹,不写作法).
(2)【应用与证明】求证:$CD// AB$.

答案:
(1)如图所示.
(2)在△CDA和△ABC中,
$\left\{ \begin{array} { l } { A D = C B , } \\ { \angle C A D = \angle A C B , } \\ { A C = C A , } \end{array} \right.$
$\therefore \triangle C D A \cong \triangle A B C .$
$\therefore \angle A C D = \angle C A B .$
$\therefore C D // A B .$

(1)如图所示.
(2)在△CDA和△ABC中,
$\left\{ \begin{array} { l } { A D = C B , } \\ { \angle C A D = \angle A C B , } \\ { A C = C A , } \end{array} \right.$
$\therefore \triangle C D A \cong \triangle A B C .$
$\therefore \angle A C D = \angle C A B .$
$\therefore C D // A B .$

5. 如图,用尺规作图“过点C作$CN// OA$”的实质就是作$∠DOM=∠NCE$,其作图依据是 (
A. SAS
B. SSS
C. ASA
D. AAS
B
)A. SAS
B. SSS
C. ASA
D. AAS
答案:
B
6. 不能用直尺和圆规作出唯一三角形的是 (
A. 已知两角和夹边
B. 已知两边和夹角
C. 已知两角和其中一角的对边
D. 已知两边和其中一边的对角
D
)A. 已知两角和夹边
B. 已知两边和夹角
C. 已知两角和其中一角的对边
D. 已知两边和其中一边的对角
答案:
D
7. 如图,已知$△ABC$,小慧同学利用直尺和圆规作出$△A_{1}B_{1}C_{1}$与其全等,根据作图痕迹可知,判定两个三角形全等的依据是
SAS
.
答案:
SAS
查看更多完整答案,请扫码查看


