第8页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
1. (2025·定西渭源期中改编)如图,将$\triangle ABC$沿着平行于 BC 的直线折叠,点 A 落到点$A'$处.若$∠C=135^{\circ },∠A=15^{\circ }$,则$∠A'DB$的度数为 (
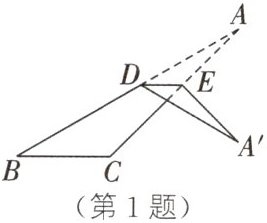
A.$90^{\circ }$
B.$100^{\circ }$
C.$110^{\circ }$
D.$120^{\circ }$
D
)
A.$90^{\circ }$
B.$100^{\circ }$
C.$110^{\circ }$
D.$120^{\circ }$
答案:
D
2. (2025·天津红桥期中)如图,在$\triangle ABC$中,$∠C=90^{\circ }$.若$∠A:∠ABC=2:1$,则$∠CBD$的度数为 (
A.$120^{\circ }$
B.$130^{\circ }$
C.$140^{\circ }$
D.$150^{\circ }$
D
)A.$120^{\circ }$
B.$130^{\circ }$
C.$140^{\circ }$
D.$150^{\circ }$
答案:
D
3. 将一副直角三角尺按如图所示的方式放置,$∠E=60^{\circ },∠C=45^{\circ },EF// BC$,则$∠BND$的度数为
$105^{\circ }$
.
答案:
$ 105 ^ { \circ } $
4. 如图,在$\triangle ABC$中,AD 是高,AE,BF 是角平分线,且相交于点 O,$∠C=70^{\circ }$.
(1)$∠AOB$的度数为____
(2)若$∠ABC=60^{\circ }$,求$∠DAE$的度数.
(1)$∠AOB$的度数为____
$125^{\circ }$
.(2)若$∠ABC=60^{\circ }$,求$∠DAE$的度数.
$ \because $ 在 $ \triangle A B C $ 中,$ A D $ 是高,$ \angle C = 70 ^ { \circ } $,$ \angle A B C = 60 ^ { \circ } $,
$ \therefore \angle D A C = 90 ^ { \circ } - \angle C = 90 ^ { \circ } - 70 ^ { \circ } = 20 ^ { \circ } $,$ \angle B A C = 180 ^ { \circ } - \angle A B C - \angle C = 180 ^ { \circ } - 60 ^ { \circ } - 70 ^ { \circ } = 50 ^ { \circ } $.
$ \because A E $ 是 $ \angle B A C $ 的平分线,
$ \therefore \angle C A E = \frac { 1 } { 2 } \angle B A C = 25 ^ { \circ } $.
$ \therefore \angle D A E = \angle C A E - \angle D A C = 25 ^ { \circ } - 20 ^ { \circ } = 5 ^ { \circ } $.
$ \therefore \angle D A C = 90 ^ { \circ } - \angle C = 90 ^ { \circ } - 70 ^ { \circ } = 20 ^ { \circ } $,$ \angle B A C = 180 ^ { \circ } - \angle A B C - \angle C = 180 ^ { \circ } - 60 ^ { \circ } - 70 ^ { \circ } = 50 ^ { \circ } $.
$ \because A E $ 是 $ \angle B A C $ 的平分线,
$ \therefore \angle C A E = \frac { 1 } { 2 } \angle B A C = 25 ^ { \circ } $.
$ \therefore \angle D A E = \angle C A E - \angle D A C = 25 ^ { \circ } - 20 ^ { \circ } = 5 ^ { \circ } $.
答案:
(1) $ 125 ^ { \circ } $.
(2) $ \because $ 在 $ \triangle A B C $ 中,$ A D $ 是高,$ \angle C = 70 ^ { \circ } $,$ \angle A B C = 60 ^ { \circ } $,
$ \therefore \angle D A C = 90 ^ { \circ } - \angle C = 90 ^ { \circ } - 70 ^ { \circ } = 20 ^ { \circ } $,$ \angle B A C = 180 ^ { \circ } - \angle A B C - \angle C = 180 ^ { \circ } - 60 ^ { \circ } - 70 ^ { \circ } = 50 ^ { \circ } $.
$ \because A E $ 是 $ \angle B A C $ 的平分线,
$ \therefore \angle C A E = \frac { 1 } { 2 } \angle B A C = 25 ^ { \circ } $.
$ \therefore \angle D A E = \angle C A E - \angle D A C = 25 ^ { \circ } - 20 ^ { \circ } = 5 ^ { \circ } $.
(1) $ 125 ^ { \circ } $.
(2) $ \because $ 在 $ \triangle A B C $ 中,$ A D $ 是高,$ \angle C = 70 ^ { \circ } $,$ \angle A B C = 60 ^ { \circ } $,
$ \therefore \angle D A C = 90 ^ { \circ } - \angle C = 90 ^ { \circ } - 70 ^ { \circ } = 20 ^ { \circ } $,$ \angle B A C = 180 ^ { \circ } - \angle A B C - \angle C = 180 ^ { \circ } - 60 ^ { \circ } - 70 ^ { \circ } = 50 ^ { \circ } $.
$ \because A E $ 是 $ \angle B A C $ 的平分线,
$ \therefore \angle C A E = \frac { 1 } { 2 } \angle B A C = 25 ^ { \circ } $.
$ \therefore \angle D A E = \angle C A E - \angle D A C = 25 ^ { \circ } - 20 ^ { \circ } = 5 ^ { \circ } $.
5. (2024·宜宾叙州期末改编)如图,在三角形纸片 ABC 中,$∠A=90^{\circ },∠B=68^{\circ }$,D 为边AC 上靠近点 C 的一定点,E 为边 BC 上的一动点,沿 DE 折叠三角形纸片,当点 C 落在$\triangle ABC$内部的点$C'$处时,$∠ADC'+∠BEC'$等于 (
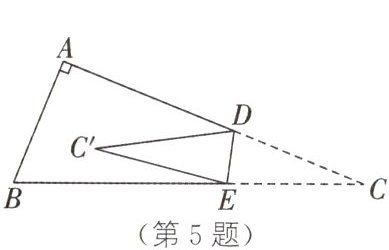
A.$22^{\circ }$
B.$33^{\circ }$
C.$44^{\circ }$
D.$68^{\circ }$
C
)
A.$22^{\circ }$
B.$33^{\circ }$
C.$44^{\circ }$
D.$68^{\circ }$
答案:
C
6. 如图,$∠A=65^{\circ },∠B=40^{\circ },∠C=25^{\circ }$,则$∠D+∠E$的度数为 (
A.$25^{\circ }$
B.$40^{\circ }$
C.$50^{\circ }$
D.$65^{\circ }$
C
)A.$25^{\circ }$
B.$40^{\circ }$
C.$50^{\circ }$
D.$65^{\circ }$
答案:
C
7. 如图,在$\triangle ABC$中,O 是三个内角的平分线的交点,过点 O 作$∠ODC=∠AOC$,交边BC 于点 D. 若$∠ABC=n^{\circ }$,则$∠BOD$的度数为 (
A.$90^{\circ }+\frac {1}{2}n^{\circ }$
B.$45^{\circ }+\frac {1}{2}n^{\circ }$
C.$90^{\circ }-\frac {1}{2}n^{\circ }$
D.$90^{\circ }$
D
)A.$90^{\circ }+\frac {1}{2}n^{\circ }$
B.$45^{\circ }+\frac {1}{2}n^{\circ }$
C.$90^{\circ }-\frac {1}{2}n^{\circ }$
D.$90^{\circ }$
答案:
D 解析:$ \because \angle A B C = n ^ { \circ } $,
$ \therefore \angle B A C + \angle B C A = 180 ^ { \circ } - \angle A B C = 180 ^ { \circ } - n ^ { \circ } $. $ \because O $ 是三个内角的平分线的交点,$ \therefore \angle O B C = \frac { 1 } { 2 } \angle A B C = \frac { 1 } { 2 } n ^ { \circ } $,$ \angle O C A = \frac { 1 } { 2 } \angle B C A $,$ \angle O A C = \frac { 1 } { 2 } \angle B A C $. $ \therefore \angle O A C + \angle O C A = \frac { 1 } { 2 } ( \angle B A C + \angle B C A ) = \frac { 1 } { 2 } ( 180 ^ { \circ } - n ^ { \circ } ) = 90 ^ { \circ } - \frac { 1 } { 2 } n ^ { \circ } $. $ \therefore \angle A O C = 180 ^ { \circ } - ( \angle O A C + \angle O C A ) = 180 ^ { \circ } - ( 90 ^ { \circ } - \frac { 1 } { 2 } n ^ { \circ } ) = 90 ^ { \circ } + \frac { 1 } { 2 } n ^ { \circ } $. $ \because \angle O D C = \angle A O C $,$ \therefore \angle O D C = 90 ^ { \circ } + \frac { 1 } { 2 } n ^ { \circ } $.
$ \therefore \angle B D O = 180 ^ { \circ } - \angle O D C = 180 ^ { \circ } - ( 90 ^ { \circ } + \frac { 1 } { 2 } n ^ { \circ } ) = 90 ^ { \circ } - \frac { 1 } { 2 } n ^ { \circ } $. $ \because \angle O B C = \frac { 1 } { 2 } n ^ { \circ } $,$ \therefore \angle B O D = 180 ^ { \circ } - \angle B D O - \angle O B C = 90 ^ { \circ } $.
$ \therefore \angle B A C + \angle B C A = 180 ^ { \circ } - \angle A B C = 180 ^ { \circ } - n ^ { \circ } $. $ \because O $ 是三个内角的平分线的交点,$ \therefore \angle O B C = \frac { 1 } { 2 } \angle A B C = \frac { 1 } { 2 } n ^ { \circ } $,$ \angle O C A = \frac { 1 } { 2 } \angle B C A $,$ \angle O A C = \frac { 1 } { 2 } \angle B A C $. $ \therefore \angle O A C + \angle O C A = \frac { 1 } { 2 } ( \angle B A C + \angle B C A ) = \frac { 1 } { 2 } ( 180 ^ { \circ } - n ^ { \circ } ) = 90 ^ { \circ } - \frac { 1 } { 2 } n ^ { \circ } $. $ \therefore \angle A O C = 180 ^ { \circ } - ( \angle O A C + \angle O C A ) = 180 ^ { \circ } - ( 90 ^ { \circ } - \frac { 1 } { 2 } n ^ { \circ } ) = 90 ^ { \circ } + \frac { 1 } { 2 } n ^ { \circ } $. $ \because \angle O D C = \angle A O C $,$ \therefore \angle O D C = 90 ^ { \circ } + \frac { 1 } { 2 } n ^ { \circ } $.
$ \therefore \angle B D O = 180 ^ { \circ } - \angle O D C = 180 ^ { \circ } - ( 90 ^ { \circ } + \frac { 1 } { 2 } n ^ { \circ } ) = 90 ^ { \circ } - \frac { 1 } { 2 } n ^ { \circ } $. $ \because \angle O B C = \frac { 1 } { 2 } n ^ { \circ } $,$ \therefore \angle B O D = 180 ^ { \circ } - \angle B D O - \angle O B C = 90 ^ { \circ } $.
8. (2024·聊城期末改编)如图,在$\triangle ABC$中,BD 是边 AC 上的高,CE 是$∠ACB$的平分线,BD,CE 相交于点 F. 若$∠AEC=80^{\circ },$$∠BFC=128^{\circ }$,则$∠ABC$的度数为____
$42^{\circ }$
.
答案:
$ 42 ^ { \circ } $ 解析:$ \because B D $ 是边 $ A C $ 上的高,$ \therefore \angle B D C = 90 ^ { \circ } $. 又 $ \because \angle B F C = 128 ^ { \circ } $,$ \therefore \angle C F D = 180 ^ { \circ } - \angle B F C = 52 ^ { \circ } $. $ \therefore \angle A C E = 90 ^ { \circ } - \angle C F D = 90 ^ { \circ } - 52 ^ { \circ } = 38 ^ { \circ } $. 又 $ \because \angle A E C = 80 ^ { \circ } $,$ \therefore \angle A = 180 ^ { \circ } - \angle A E C - \angle A C E = 180 ^ { \circ } - 80 ^ { \circ } - 38 ^ { \circ } = 62 ^ { \circ } $. 又 $ \because C E $ 是 $ \angle A C B $ 的平分线,$ \therefore \angle A C B = 2 \angle A C E = 76 ^ { \circ } $.
$ \therefore \angle A B C = 180 ^ { \circ } - \angle A - \angle A C B = 180 ^ { \circ } - 62 ^ { \circ } - 76 ^ { \circ } = 42 ^ { \circ } $.
$ \therefore \angle A B C = 180 ^ { \circ } - \angle A - \angle A C B = 180 ^ { \circ } - 62 ^ { \circ } - 76 ^ { \circ } = 42 ^ { \circ } $.
查看更多完整答案,请扫码查看


