第27页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
1.在△ABC和△A'B'C'中,AB= A'B',∠A= ∠A',∠B= ∠B',则△ABC≌△A'B'C'的根据是(
A.SAS
B.SSS
C.ASA
D.都行
C
)A.SAS
B.SSS
C.ASA
D.都行
答案:
C
2.如图,已知△ABC三条边、三个角,则甲、乙两个三角形中和△ABC全等的图形是(
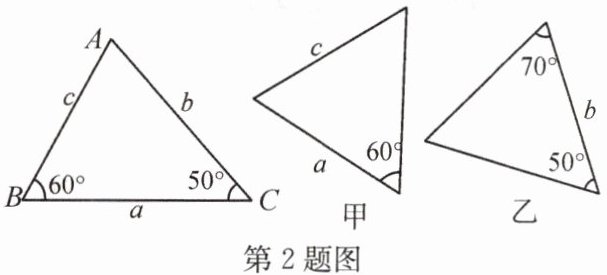
A.甲
B.乙
C.甲和乙
D.都不是
B
)
A.甲
B.乙
C.甲和乙
D.都不是
答案:
B
3.(2022·洪山)如图,E,B,C,F在一条直线上,EB= CF,∠A= ∠D,再添一个条件仍不能证明△ABC≌△DEF的是(

A.AB= DE
B.DF//AC
C.∠E= ∠ABC
D.AB//DE
A
)
A.AB= DE
B.DF//AC
C.∠E= ∠ABC
D.AB//DE
答案:
A
4.一块三角形的玻璃,摔成甲乙两块,现在想还原一块一样的玻璃,则需拿
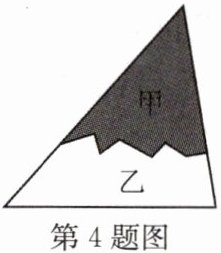
乙
去玻璃店,理由是ASA
.
答案:
乙 ASA
5.如图,∠ABC= ∠DEF,AB= DE,要使△ABC≌△DEF.
(1)若以“ASA”为依据,还需添加的条件为
(2)若以“AAS”为依据,还需添加的条件为
(1)若以“ASA”为依据,还需添加的条件为
∠A=∠D
;(2)若以“AAS”为依据,还需添加的条件为
∠ACB=∠DFE
.
答案:
(1)$∠A=∠D$;
(2)$∠ACB=∠DFE$。
(1)$∠A=∠D$;
(2)$∠ACB=∠DFE$。
6.如图,AB= CD,点D在OA上,点B在OC上,∠A= ∠C.
(1)求证:△AOB≌△COD; 证明:
(2)求证:AD= BC.证明:

(1)求证:△AOB≌△COD; 证明:
$\left\{\begin{array}{l} ∠A=∠C\\ ∠O=∠O,\\ AB=CD\end{array}\right. $$\therefore △AOB\cong △COD(AAS)$
(2)求证:AD= BC.证明:
由(1)知$OA=OC$,$OD=OB$,$\therefore AD=BC$

答案:
证明:
(1)$\left\{\begin{array}{l} ∠A=∠C\\ ∠O=∠O,\\ AB=CD\end{array}\right. $
$\therefore △AOB\cong △COD(AAS)$;
(2)由
(1)知$OA=OC$,
$OD=OB$,$\therefore AD=BC$。
(1)$\left\{\begin{array}{l} ∠A=∠C\\ ∠O=∠O,\\ AB=CD\end{array}\right. $
$\therefore △AOB\cong △COD(AAS)$;
(2)由
(1)知$OA=OC$,
$OD=OB$,$\therefore AD=BC$。
7.(2020·广州)如图,点D是AB上一点,DF交AC于点E,DE= FE,FC//AB,求证:△ADE≌△CFE.
证明:∵FC// AB,
∴∠A=∠ACF,
∠ADE=∠F,
又DE=EF,
∴△ADE≌△CFE
证明:∵FC// AB,
∴∠A=∠ACF,
∠ADE=∠F,
又DE=EF,
∴△ADE≌△CFE
(AAS)
.
答案:
解:$\because FC// AB$,
$\therefore ∠A=∠ACF$,
$∠ADE=∠F$,
又$DE=EF$,
$\therefore △ADE\cong △CFE$。
$\therefore ∠A=∠ACF$,
$∠ADE=∠F$,
又$DE=EF$,
$\therefore △ADE\cong △CFE$。
8.如图,四边形ABCD中,AB//CD,点E在AC上,∠1= ∠2,AC= AB,求证:CD= AE.
证明:
∴ CD=AE。
证明:
△ACD≌△BAE(ASA)
,∴ CD=AE。
答案:
证明:$△ACD\cong △BAE(ASA)$,
$\therefore CD=AE$。
$\therefore CD=AE$。
查看更多完整答案,请扫码查看


