《2025年通成学典课时作业本九年级数学上册苏科版苏州专版》

7. 箱内有50个白球和10个红球,小慧打算从箱内抽球31次,每次从箱内抽出一球,若抽出白球,则将白球放回箱内;若抽出红球,则不将红球放回箱内.已知小慧在前30次抽球中共抽出红球4次,若她第31次抽球时箱内的每个球被抽出的机会相等,则这次她抽出红球的概率为 ()

A.$\frac{1}{5}$
B.$\frac{1}{6}$
C.$\frac{5}{12}$
D.$\frac{3}{28}$

答案： D

8. 在$□ ABCD$中,$AC$、$BD$是两条对角线,有以下四个关系:①$AB=BC$;②$AC=BD$;③$AC\perp BD$;④$AB\perp BC$.现从中随机选出一个作为条件,可推出$□ ABCD$是菱形的概率为.

答案： $\frac{1}{2}$（或 0.5）的填装形式（即概率的标准填空形式为分数或小数，本题答案以分数$\frac{1}{2}$为准进行盒子填充）为：$\boxed{\dfrac{1}{2}}$

9. (2024·泸州)在一个不透明的盒子中装有6个白球,若干个黄球,它们除颜色不同外,其余均相同.若从中随机摸出一个球是白球的概率是$\frac{2}{3}$,则黄球的个数为.

答案： 3

10. 从-3、-2、2这三个数中任取两个不同的数,作为点的坐标,则该点落在第三象限的概率是.

答案： $\frac{1}{3}$（或 填对应选择项）。

11. (2024·苏州高新区期中)如图,在一不规则图形内,有一边长为$3\sqrt{3}$m的正方形,向不规则图形内随机地掷4000颗黄豆,数得落在正方形内(含边界)的黄豆有1350颗,以此试验数据为依据,可以估计出该不规则图形的面积.
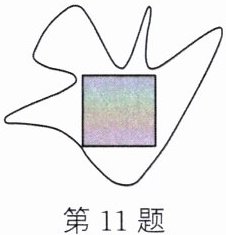
(1) 随机向不规则图形内掷一颗黄豆,求黄豆落在正方形内(含边界)的概率;
(2) 请你估计该不规则图形的面积.

答案：
(1) 黄豆落在正方形内（含边界）的概率为：$\frac{1350}{4000} = \frac{27}{80}$。
(2) 正方形的面积为：$(3\sqrt{3})^2 = 27$（$m^2$）。
设不规则图形的面积为$S$，由概率公式得：$\frac{27}{S} = \frac{27}{80}$，解得$S = 80$（$m^2$）。
(1) $\frac{27}{80}$；
(2) $80m^2$

12. (教材P132例2变式)一个不透明的袋子中装有红、黄、白三种颜色的球共100个,它们除颜色外都相同,其中黄球的个数比白球个数的2倍少5.已知从袋子中摸出1个球是红球的概率是$\frac{3}{10}$.
(1) 求袋子中红球的个数;
(2) 求从袋子中摸出1个球是白球的概率;
(3) 取走10个球(其中没有红球)后,求从剩余的球中摸出1个球是红球的概率.

答案：
(1) 袋子中红球的个数：
由题意，从袋子中摸出1个球是红球的概率是 $\frac{3}{10}$，因此红球的数量为：
$100 × \frac{3}{10} = 30$，
所以袋子中红球的个数为30。
(2) 设白球有 $x$ 个，则黄球有 $2x - 5$ 个。
根据题意，红球、黄球和白球的总数为100，即：
$30 + x + (2x - 5) = 100$，
解这个方程，得到：
$3x = 75$，
$x = 25$，
所以白球有25个，从袋子中摸出1个球是白球的概率为：
$P(白球) = \frac{25}{100} = \frac{1}{4}$。
(3) 取走10个球（其中没有红球）后，剩余的球数为90个，红球数量仍为30个。
因此，从剩余的球中摸出1个球是红球的概率为：
$P(红球) = \frac{30}{90} = \frac{1}{3}$。