《2025年通成学典课时作业本九年级数学上册苏科版苏州专版》

14. 若$x=t$是关于x的一元二次方程$ax^{2}+bx+c=0(a≠0)$的根,$M=(2at+b)^{2}$,则根的判别式$b^{2}-4ac$和M的大小关系是()

A.$b^{2}-4ac=M$
B.$b^{2}-4ac＞M$
C.$b^{2}-4ac＜M$
D.无法确定

答案： A

15. (2024·凉山)已知$y^{2}-x=0,x^{2}-3y^{2}+x-3=0$,则x的值为.

答案： $3$

16. (2023·泸州)若一个菱形的两条对角线的长分别是关于x的方程$x^{2}-10x+m=0$的两个实数根,且其面积为11,则该菱形的边长为.

答案： $\sqrt{14}$

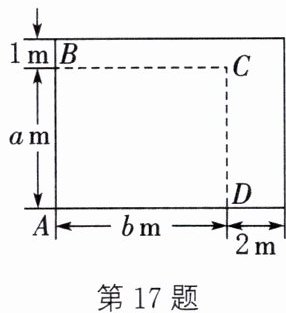
17. (2023·金华)如图所示为一块矩形菜地ABCD,$AB=am,AD=bm$,面积为$s{m}^{2}$,现将边AB的长增加1m,边AD的长增加2m.若有且只有一个a的值,使得到的新矩形菜地的面积为$2sm^{2}$,则s的值为.

答案： $6 + 4\sqrt{2}$

18. 已知$x_{1}$、$x_{2}$是关于x的一元二次方程$x^{2}-2(m+1)x+m^{2}+5=0$的两个实数根.
(1)若$(x_{1}-1)(x_{2}-1)=28$,则m的值为.
(2)已知等腰三角形ABC的一边长为7.若$x_{1}$、$x_{2}$恰好是$\triangle ABC$的另外两边的长,求这个三角形的周长.

答案：
(1)
根据韦达定理，对于一元二次方程$ax^2 + bx + c = 0$，两根$x_1$、$x_2$有$x_1 + x_2 = -\frac{b}{a}$，$x_1x_2 = \frac{c}{a}$。
对于方程$x^{2}-2(m + 1)x + m^{2}+5 = 0$，$a = 1$，$b = -2(m + 1)$，$c = m^{2}+5$，则$x_1 + x_2 = 2(m + 1)$，$x_1x_2 = m^{2}+5$。
已知$(x_1 - 1)(x_2 - 1)=28$，展开可得$x_1x_2-(x_1 + x_2)+1 = 28$。
将$x_1 + x_2 = 2(m + 1)$，$x_1x_2 = m^{2}+5$代入上式得：
$m^{2}+5-2(m + 1)+1 = 28$，
$m^{2}+5-2m-2 + 1 = 28$，
$m^{2}-2m-24 = 0$，
$(m - 6)(m + 4)=0$，
解得$m_1 = 6$，$m_2=-4$。
方程有实数根，则判别式$\Delta=b^{2}-4ac\geqslant0$，
$\Delta =[-2(m + 1)]^{2}-4(m^{2}+5)\geqslant0$，
$4(m^{2}+2m + 1)-4m^{2}-20\geqslant0$，
$4m^{2}+8m+4-4m^{2}-20\geqslant0$，
$8m-16\geqslant0$，
$8m\geqslant16$，
$m\geqslant2$。
所以$m$的值为$6$。
(2)
当$7$为底边时，$x_1 = x_2$，此时$\Delta = 0$，
由$\Delta =[-2(m + 1)]^{2}-4(m^{2}+5)=0$，
$4(m^{2}+2m + 1)-4m^{2}-20 = 0$，
$8m-16 = 0$，
$m = 2$。
方程为$x^{2}-6x + 9 = 0$，
$(x - 3)^{2}=0$，
$x_1 = x_2 = 3$。
因为$3 + 3\lt7$，不满足三角形三边关系，舍去。
当$7$为腰时，设$x_1 = 7$，代入方程$x^{2}-2(m + 1)x + m^{2}+5 = 0$得：
$49-14(m + 1)+m^{2}+5 = 0$，
$m^{2}-14m + 40 = 0$，
$(m - 4)(m - 10)=0$，
解得$m_1 = 4$，$m_2 = 10$。
当$m = 4$时，方程为$x^{2}-10x + 21 = 0$，
$(x - 3)(x - 7)=0$，
$x_1 = 3$，$x_2 = 7$。
此时三角形三边为$7$，$7$，$3$，满足三边关系，周长为$7 + 7+3 = 17$。
当$m = 10$时，方程为$x^{2}-22x + 105 = 0$，
$(x - 7)(x - 15)=0$，
$x_1 = 7$，$x_2 = 15$。
因为$7 + 7\lt15$，不满足三角形三边关系，舍去。
综上，这个三角形的周长为$17$。

19. (新情境·现实生活)某汽车销售公司6月销售某厂家的汽车,在一定范围内,每辆汽车的进价与销售量有如下关系:若当月仅销售1辆汽车,则该辆汽车的进价为27万元,每多销售1辆,所有销售的汽车每辆的进价均降低0.1万元.月底厂家根据销售量一次性返利给销售公司,销售10辆以内(含10辆),每辆返利0.5万元;销售10辆以上,每辆返利1万元.
(1)若该汽车销售公司当月销售3辆该厂家汽车,则每辆汽车的进价为万元;
(2)若每辆汽车的售价为28万元,该汽车销售公司计划当月盈利12万元,则需要销售多少辆汽车(盈利=销售利润+返利)?

答案：
(1)
根据题意，若当月仅销售$1$辆汽车，进价为$27$万元，每多销售$1$辆，所有销售的汽车每辆进价均降低$0.1$万元。
当销售$3$辆汽车时，进价降低$0.1×(3 - 1)= 0.2$万元。
所以每辆汽车的进价为$27-0.2 = 26.8$万元。
(2)
设需要销售$x$辆汽车。
每辆汽车的销售利润为$28-[27 - 0.1(x - 1)]=(0.1x + 0.9)$万元。
当$0\lt x\leq10$时，根据盈利公式：盈利$=$销售利润$+$返利，可列方程：
$(0.1x + 0.9)x+0.5x = 12$，
整理得$x^{2}+14x - 120=0$，
因式分解为$(x + 20)(x - 6)=0$，
解得$x_{1}=-20$（舍去），$x_{2}=6$。
当$x\gt10$时，可列方程：
$(0.1x + 0.9)x+x = 12$，
整理得$x^{2}+19x - 120=0$，
因式分解为$(x + 24)(x - 5)=0$（经检验，此处因式分解应为$(x - 5)(x+24)=x^{2}+19x - 120$），
解得$x_{1}=-24$（舍去），$x_{2}=5$，因为$5\lt10$，不符合$x\gt10$的条件，舍去。
综上，需销售$6$辆汽车。