《2025年通成学典课时作业本九年级数学上册苏科版苏州专版》

8. 如图，AB是⊙O的直径，弦CD⊥AB，垂足为E，连接AC.若∠CAB=22.5°，CD=8 cm，则⊙O的半径为cm.

答案： 4√2

9. 如图，在⊙O中，⌢AB=2⌢AC，AD⊥OC于点D.若AB=8，则AD的长为.

答案： 4

10. 已知⊙O的直径为20，弦AB的长为12，P是弦AB上一动点，则满足线段OP的长为整数的点P有处不同的位置.

答案： 5

11. 如图，在Rt△ABC中，∠C=90°，以点C为圆心、AC为半径的⊙C与AB相交于点D.若AC=6，BC=8，则AD的长为.

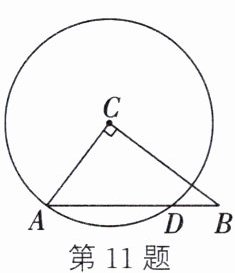
答案： $7.2$

12. (新情境·现实生活)(2023·广西改编)如图，某地有一座圆弧形拱桥，桥拱所在圆的圆心为点O，桥下水面的宽度AB为7.2 m，过点O作OC⊥AB于点D，交圆弧于点C，CD=2.4 m.现有一艘宽3 m、船舱顶部高出水面AB 2 m的货船要经过这座拱桥，此货船能否顺利通过这座拱桥?

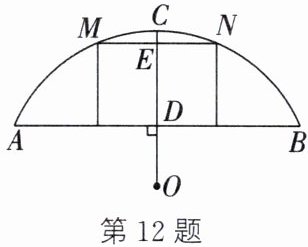
答案： 设桥拱所在圆的半径为 $R$ m。
在$Rt \bigtriangleup OBD$中，由题意可得：
$BD=\frac{1}{2}AB = 3.6$（m），
$OD = R - CD = R - 2.4$（m）。
根据勾股定理，$OB^{2} = BD^{2} + OD^{2}$，
即$R^{2} = 3.6^{2} + (R - 2.4)^{2}$。
展开并化简得：
$R^{2} = 12.96 + R^{2} - 4.8R + 5.76$，
$4.8R = 18.72$，
解得$R = 3.9$。
当货船宽3m时，假设货船恰好通过，此时船两侧与桥拱接触点关于$y$轴对称，设接触点为$M$，$N$，过$M$作$ME\bot AB$于$E$，过$O$作$OC\bot MN$于$C$（$C$在$MN$延长线上），则$ME = 2$m，$MN = 3$m，所以$EN=\frac{1}{2}MN = 1.5$m。
在$Rt \bigtriangleup OEN$中，$ON = OB = 3.9$m，$EN = 1.5$m，根据勾股定理可得：
$OE=\sqrt{ON^{2}-EN^{2}}=\sqrt{3.9^{2} - 1.5^{2}}=\sqrt{15.21 - 2.25}=\sqrt{12.96}= 3.6$（m）。
则$OD + 2=3.9 - 2.4+2 = 3.5\lt 3.6$。
所以此货船能顺利通过这座拱桥。

13. (2024·包头)如图，AB是⊙O的直径，BC、BD是⊙O的两条弦，点C与点D在AB的两侧，E是OB上一点(OE＞BE)，连接OC、CE.若∠BOC=2∠BCE，且BD=2OE.求证：BD//OC.

答案： 证明：设∠BCE=x，则∠BOC=2x。
∵OC=OB，
∴△OBC为等腰三角形，∠OCB=∠OBC。
∵∠BOC+∠OCB+∠OBC=180°，
∴2∠OCB+2x=180°，∠OCB=90°-x。
∵∠OCB=∠OCE+∠BCE，∠BCE=x，
∴∠OCE=∠OCB-x=90°-2x。
在△OCE中，∠COE=∠BOC=2x，∠OCE=90°-2x，
∴∠OEC=180°-∠COE-∠OCE=180°-2x-(90°-2x)=90°，即CE⊥OB。
设OE=m，则BD=2m。过O作OF⊥BD于F，由垂径定理得BF=FD=BD/2=m。
在Rt△OCE中，OC²=OE²+CE²，即CE²=OC²-m²。
在Rt△OFB中，OB²=OF²+BF²，OB=OC，BF=m，
∴OF²=OC²-m²=CE²，故OF=CE。
∵CE⊥OB，OF⊥BD，
∴∠OEC=∠OFB=90°。
在Rt△OCE和Rt△BOF中，sin∠COE=CE/OC，sin∠OBF=OF/OB，
∵CE=OF，OC=OB，
∴sin∠COE=sin∠OBF。
∵∠COE=2x＜90°（∠OCE=90°-2x＞0），∠OBF为锐角，
∴∠OBF=∠COE=2x。
∵∠COB=∠OBF=2x（内错角相等），
∴BD//OC。
结论：BD//OC。