《2025年通成学典课时作业本九年级数学上册苏科版苏州专版》

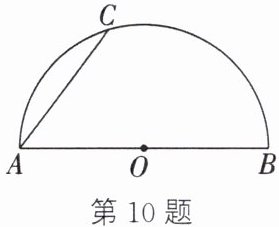
10.（2025·太仓期末）如图，$AB$是半圆的直径，点$O$为圆心，$C$是半圆上一点，连接$AC$.
（1）用无刻度的直尺和圆规作图：在半圆上确定一点$P$，使得$\overset{\frown}{PB}=\overset{\frown}{PC}$（保留作图痕迹）.
（2）在（1）的条件下，连接$PB$、$PC$.若$AB=10$，$AC=6$，求四边形$ABPC$的面积.

答案： （2）32

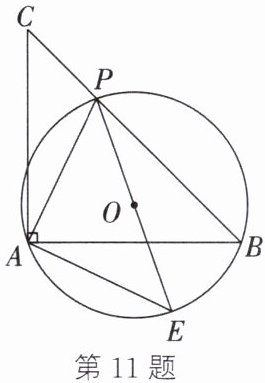
11. 如图，在等腰直角三角形$ABC$中，$\angle BAC=90^{\circ}$，$P$是斜边$BC$上一点（不与点$B$、$C$重合），$PE$是$\triangle ABP$的外接圆$\odot O$的直径，连接$AP$、$AE$.
（1）求证：$\triangle APE$是等腰直角三角形；
（2）若$\odot O$的直径为2，求$PC^{2}+PB^{2}$的值.

答案： （1）见解析；（2）4。

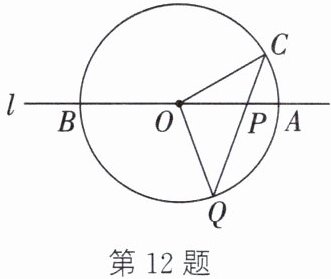
12. 如图，直线$l$经过$\odot O$的圆心，且交$\odot O$于$A$、$B$两点，点$C$在$\odot O$上，且$\angle AOC=30^{\circ}$，$P$是直线$l$上的一个动点（不与圆心$O$重合），$CP$与$\odot O$相交于另一点$Q$，连接$QO$.若$QP=QO$，求$\angle OCP$的度数.

答案： 情况一：点P在点O右侧（A点所在一侧）
设∠OCP=x，∠QOP=α。
∵Q在⊙O上，
∴QO=OC（半径相等），△OCQ为等腰三角形，∠OCQ=∠OQC=x，故∠COQ=180°-2x。
∵QP=QO，
∴△QOP为等腰三角形，∠QOP=∠QPO=α，故∠OQP=180°-2α。
∵C，Q，P共线，
∴∠OQC+∠OQP=180°，即x+(180°-2α)=180°，得x=2α。
∵∠AOC=30°，∠COQ=∠AOC+∠AOQ，∠AOQ=α，
∴180°-2x=30°+α。
将α=x/2代入，得180°-2x=30°+x/2，解得x=60°。
情况二：点P在点O左侧（B点所在一侧）
设∠OCP=x，∠QOP=α。
同理，△OCQ中∠COQ=180°-2x，△QOP中∠QOP=∠QPO=α，∠OQP=180°-2α。
∵C，Q，P共线，∠OQC=∠OQP+∠CQP（补角关系），得x=2α。
∵∠AOC=30°，∠COQ=∠AOQ-∠AOC，∠AOQ=180°-α，
∴180°-2x=(180°-α)-30°。
将α=x/2代入，得180°-2x=150°-x/2，解得x=20°。
结论：∠OCP的度数为20°或60°。
20°或60°