第32页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
8. (2023·达州)已知$x_{1}$、$x_{2}$是方程$2x^{2}+kx-2=0$的两个实数根,且$(x_{1}-2)(x_{2}-2)=10$,则k的值为.
答案:
7
9. (2024·泸州)已知$x_{1}$、$x_{2}$是一元二次方程$x^{2}-3x-5=0$的两个实数根,则$(x_{1}-x_{2})^{2}+3x_{1}x_{2}$的值是.
答案:
14
10. (2024·成都)若m、n是一元二次方程$x^{2}-5x+2=0$的两个实数根,则$m+(n-2)^{2}$的值为.
答案:
7
11. 已知关于x的一元二次方程$x^{2}-6x+m+4=0$有两个实数根$x_{1}$、$x_{2}$.
(1)求m的取值范围;
(2)若$x_{1}$、$x_{2}$满足$3x_{1}=|x_{2}|+2$,求m的值.
(1)求m的取值范围;
(2)若$x_{1}$、$x_{2}$满足$3x_{1}=|x_{2}|+2$,求m的值.
答案:
(1)m≤5;
(2)m=4。
(1)m≤5;
(2)m=4。
12. (2024·苏州工业园区期中)某中学组织九年级学生进行篮球比赛,以班为单位,每两班之间都比赛一场,计划安排15场比赛,则共有个班参赛.
答案:
6
13. (新考法·综合与实践)某校为培育青少年科技创新能力,举办了动漫制作活动,小明设计了点做圆周运动的一个雏形,如图,甲、乙两点分别从直径的两端点A、B按顺时针、逆时针的方向同时沿圆周运动,甲运动的路程$l(cm)$与时间$t(s)$满足关系:$l=\frac {1}{2}t^{2}+\frac {3}{2}t(t≥0)$,乙以4 cm/s的速度匀速运动,半圆弧的长度为21 cm.
(1)求甲运动4s的路程.
(2)甲、乙从开始运动到第一次相遇,它们运动了多长时间?
(3)甲、乙从开始运动到第二次相遇,它们运动了多长时间?
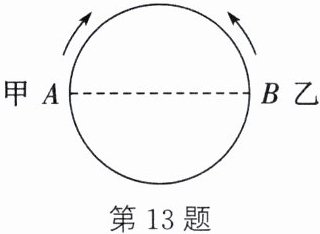
(1)求甲运动4s的路程.
(2)甲、乙从开始运动到第一次相遇,它们运动了多长时间?
(3)甲、乙从开始运动到第二次相遇,它们运动了多长时间?

答案:
(1)当$t=4$时,甲的路程$l=\frac{1}{2}×4^{2}+\frac{3}{2}×4=\frac{1}{2}×16+\frac{3}{2}×4=8 + 6=14\,cm$。
(2)设第一次相遇时间为$t_1\,s$。甲路程$l_{甲}=\frac{1}{2}t_1^{2}+\frac{3}{2}t_1$,乙路程$l_{乙}=4t_1$。相遇时路程和为半圆弧长$21\,cm$,则$\frac{1}{2}t_1^{2}+\frac{3}{2}t_1 + 4t_1=21$。整理得$t_1^{2}+11t_1 - 42=0$,解得$t_1=3$($t_1=-14$舍去)。
(3)设第二次相遇时间为$t_2\,s$。相遇时路程和为$21 + 42=63\,cm$,则$\frac{1}{2}t_2^{2}+\frac{3}{2}t_2 + 4t_2=63$。整理得$t_2^{2}+11t_2 - 126=0$,解得$t_2=7$($t_2=-18$舍去)。
(1)$14\,cm$;
(2)$3\,s$;
(3)$7\,s$。
(1)当$t=4$时,甲的路程$l=\frac{1}{2}×4^{2}+\frac{3}{2}×4=\frac{1}{2}×16+\frac{3}{2}×4=8 + 6=14\,cm$。
(2)设第一次相遇时间为$t_1\,s$。甲路程$l_{甲}=\frac{1}{2}t_1^{2}+\frac{3}{2}t_1$,乙路程$l_{乙}=4t_1$。相遇时路程和为半圆弧长$21\,cm$,则$\frac{1}{2}t_1^{2}+\frac{3}{2}t_1 + 4t_1=21$。整理得$t_1^{2}+11t_1 - 42=0$,解得$t_1=3$($t_1=-14$舍去)。
(3)设第二次相遇时间为$t_2\,s$。相遇时路程和为$21 + 42=63\,cm$,则$\frac{1}{2}t_2^{2}+\frac{3}{2}t_2 + 4t_2=63$。整理得$t_2^{2}+11t_2 - 126=0$,解得$t_2=7$($t_2=-18$舍去)。
(1)$14\,cm$;
(2)$3\,s$;
(3)$7\,s$。
查看更多完整答案,请扫码查看


