《2025年通成学典课时作业本九年级数学上册苏科版苏州专版》

1. 某校健美操队共有10名队员,统计队员的年龄情况,结果如下:13岁3人,14岁5人,15岁2人.该健美操队队员的平均年龄为()

A.14.2岁
B.14.1岁
C.13.9岁
D.13.7岁

答案： C

2. (2024·德阳)某校拟招聘一名优秀的数学教师,设置了笔试、面试、试讲三项水平测试,综合成绩按照笔试占30%,面试占30%,试讲占40%进行计算,小徐的三项测试成绩依次是86分、80分、90分,则她的综合成绩为()

A.85分
B.85.3分
C.85.5分
D.85.8分

答案： D

3. (教材P102习题3.1第3题变式)(2023·大庆)某校为了解学生本学期参加志愿服务的情况,随机调查了部分学生,如图所示为调查结果的统计图,则受调查的学生本学期参加志愿服务的平均次数为.

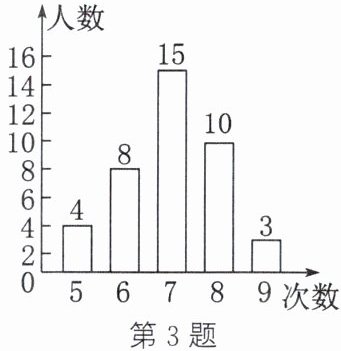
答案： 7

4. 某计算机程序第一次算得m个数据的平均数为x,第二次算得另外n个数据的平均数为y,则这$(m+n)$个数据的平均数为.

答案： $\frac{mx + ny}{m + n}$（由于题目要求答案格式，且原题为填空题形式，此处答案以表达式形式给出，若转化为选择题选项则应为对应表达式的选项）。

5. 某校学生会要在甲、乙两名候选人中选择一人担任文艺部干事,对他们进行了文化水平、艺术水平、组织能力的测试,根据综合成绩择优录取,他们的各项成绩(单项满分100分)如下表:

(1) 如果把各项成绩的平均数作为综合成绩,应该录取谁?
(2) 如果想录取一名组织能力较强的候选人,把文化水平、艺术水平、组织能力三项成绩按照1:1:3确定每个人的综合成绩,应该录取谁?

答案：
(1) 甲的平均数：
$\overline{x}_{甲} = \frac{80 + 87 + 82}{3} = \frac{249}{3} = 83$（分），
乙的平均数：
$\overline{x}_{乙} = \frac{80 + 96 + 76}{3} = \frac{252}{3} = 84$（分），
因为 $\overline{x}_{乙} ＞ \overline{x}_{甲}$，
所以应该录取乙。
(2) 甲的综合成绩：
$x_{甲} = \frac{80 × 1 + 87 × 1 + 82 × 3}{1 + 1 + 3} = \frac{80 + 87 + 246}{5} = \frac{413}{5} = 82.6$（分），
乙的综合成绩：
$x_{乙} = \frac{80 × 1 + 96 × 1 + 76 × 3}{1 + 1 + 3} = \frac{80 + 96 + 228}{5} = \frac{404}{5} = 80.8$（分），
因为 $x_{甲} ＞ x_{乙}$，
所以应该录取甲。