第77页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
20. 如图,AB是⊙O的弦,OC⊥AB,垂足为C,OD//AB,交⊙O于点D,OD=2OC,则∠ABD的度数为.
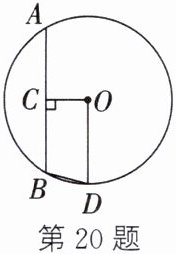

答案:
15°
21. (整体思想)(2024·资阳)如图,在矩形ABCD中,AB=4,AD=2.以点A为圆心,AD为半径作弧交AB于点E,再以AB为直径作半圆,与$\overset{\frown}{DE}$交于点F,则图中涂色部分的面积为.
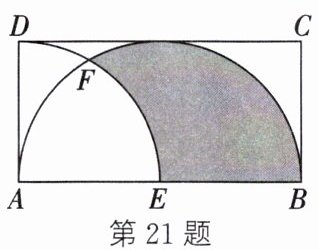

答案:
4π/3 - √3
22. (新考向·传统文化)如图,我国古代数学家赵爽的“弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.若Rt△ABC的内切圆的半径为3,小正方形的面积为49,则大正方形的面积为.
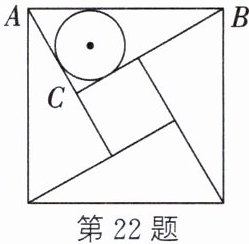

答案:
289
23. (分类讨论思想)(2024·江西)如图,AB是⊙O的直径,AB=2,点C在线段AB上运动,过点C的弦DE⊥AB,将$\overset{\frown}{DBE}$沿DE翻折交直线AB于点F.当DE的长为正整数时,线段FB的长为.
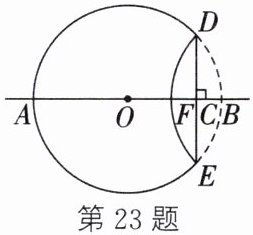

答案:
2
24. 如图,⊙O的半径为3cm,B为⊙O外一点,OB交⊙O于点A,AB=OA,动点P从点A出发,以πcm/s的速度在⊙O上按逆时针方向运动一周回到点A后停止.当点P运动的时间为s时,直线BP与⊙O相切.
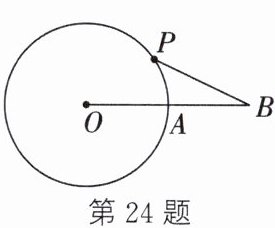

答案:
1或5
25. 如图,⊙O的半径为1,A、P、B、C是⊙O上的四个点,∠APC=∠CPB=60°.
(1) △ABC的形状是.
(2) 试探究线段PA、PB、PC之间的数量关系,并证明你的结论.
(3) 当点P位于$\overset{\frown}{AB}$的什么位置时,四边形APBC的面积最大? 请求出最大面积.
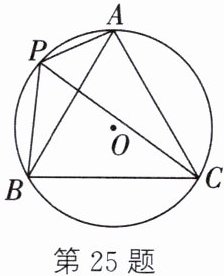
(1) △ABC的形状是.
(2) 试探究线段PA、PB、PC之间的数量关系,并证明你的结论.
(3) 当点P位于$\overset{\frown}{AB}$的什么位置时,四边形APBC的面积最大? 请求出最大面积.

答案:
(1) 等边三角形
(2) PA + PB = PC。证明:在PC上截取PD = PA,连接AD。
∵ ∠APC = 60°,PD = PA,
∴ △PAD为等边三角形,
∴ PA = AD,∠PAD = 60°。
∵ △ABC为等边三角形(已证),
∴ AB = AC,∠BAC = 60°,
∴ ∠PAB = ∠DAC(∠PAD - ∠BAD = ∠BAC - ∠BAD)。
在△APB和△ADC中,$\left\{\begin{array}{l} PA = AD \\ ∠PAB = ∠DAC \\ AB = AC \end{array}\right.$,
∴ △APB≌△ADC(SAS),
∴ PB = DC。
∵ PC = PD + DC,
∴ PC = PA + PB。
(3) 当点P位于$\overset{\frown}{AB}$的中点时,四边形APBC面积最大。
∵ 四边形APBC面积 = S△APC + S△BPC = $\frac{1}{2}PA·PC·\sin60° + \frac{1}{2}PB·PC·\sin60° = \frac{\sqrt{3}}{4}PC(PA + PB)$。
由
(2)知PA + PB = PC,
∴ 面积 = $\frac{\sqrt{3}}{4}PC^2$。
PC为⊙O的弦,当PC为直径时最长,此时PC = 2(半径为1),面积 = $\frac{\sqrt{3}}{4}×2^2 = \sqrt{3}$。
∵ P为$\overset{\frown}{AB}$中点时,PA = PB,PC为直径,
∴ 最大面积为$\sqrt{3}$。
(1) 等边三角形
(2) PA + PB = PC。证明:在PC上截取PD = PA,连接AD。
∵ ∠APC = 60°,PD = PA,
∴ △PAD为等边三角形,
∴ PA = AD,∠PAD = 60°。
∵ △ABC为等边三角形(已证),
∴ AB = AC,∠BAC = 60°,
∴ ∠PAB = ∠DAC(∠PAD - ∠BAD = ∠BAC - ∠BAD)。
在△APB和△ADC中,$\left\{\begin{array}{l} PA = AD \\ ∠PAB = ∠DAC \\ AB = AC \end{array}\right.$,
∴ △APB≌△ADC(SAS),
∴ PB = DC。
∵ PC = PD + DC,
∴ PC = PA + PB。
(3) 当点P位于$\overset{\frown}{AB}$的中点时,四边形APBC面积最大。
∵ 四边形APBC面积 = S△APC + S△BPC = $\frac{1}{2}PA·PC·\sin60° + \frac{1}{2}PB·PC·\sin60° = \frac{\sqrt{3}}{4}PC(PA + PB)$。
由
(2)知PA + PB = PC,
∴ 面积 = $\frac{\sqrt{3}}{4}PC^2$。
PC为⊙O的弦,当PC为直径时最长,此时PC = 2(半径为1),面积 = $\frac{\sqrt{3}}{4}×2^2 = \sqrt{3}$。
∵ P为$\overset{\frown}{AB}$中点时,PA = PB,PC为直径,
∴ 最大面积为$\sqrt{3}$。
查看更多完整答案,请扫码查看


