《2025年通成学典课时作业本九年级数学上册苏科版苏州专版》

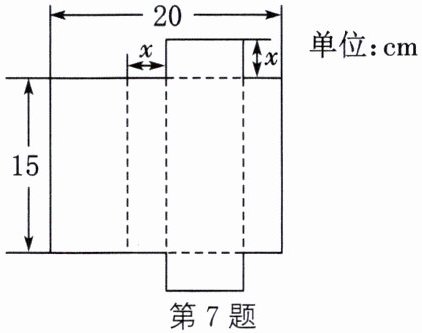
7. 将一个容积为$360\mathrm{cm}^3$的长方体包装盒剪开铺平，纸样如图所示。利用容积列出图中$x(\mathrm{cm})$满足的一元二次方程为(不必化简)。

答案： $20x(15 - x) = 360$

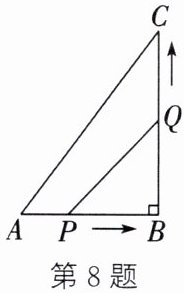
8. 如图，在$\triangle ABC$中，$\angle B = 90^{\circ}$，$AB = 6\mathrm{cm}$，$BC = 8\mathrm{cm}$。点$P$从点$A$出发，沿边$AB$向点$B$以$1\mathrm{cm}/\mathrm{s}$的速度运动，点$Q$从点$B$出发，沿边$BC$向点$C$以$2\mathrm{cm}/\mathrm{s}$的速度运动。点$P$、$Q$分别从点$A$、$B$同时出发，当点$Q$运动到点$C$时，两点同时停止运动。
（1）经过几秒，$\triangle PBQ$的面积为$8\mathrm{cm}^2$？
（2）$\triangle PBQ$的面积能为$10\mathrm{cm}^2$吗？若能，请求出此时的运动时间；若不能，请说明理由。

答案： （1）设运动时间为$ t $秒（$ 0 \leq t \leq 4 $），则$ AP = t \, cm $，$ PB = AB - AP = (6 - t) \, cm $，$ BQ = 2t \, cm $。
$\triangle PBQ$的面积$ S = \frac{1}{2} × PB × BQ = \frac{1}{2}(6 - t)(2t) = t(6 - t) $。
令$ S = 8 $，得$ t(6 - t) = 8 $，即$ t^2 - 6t + 8 = 0 $。
解得$ t_1 = 2 $，$ t_2 = 4 $，均在$ 0 \leq t \leq 4 $范围内。
故经过$ 2 $秒或$ 4 $秒。
（2）令$ S = 10 $，得$ t(6 - t) = 10 $，即$ t^2 - 6t + 10 = 0 $。
判别式$ \Delta = (-6)^2 - 4 × 1 × 10 = 36 - 40 = -4 ＜ 0 $，方程无实根。
故$\triangle PBQ$的面积不能为$ 10 \, cm^2 $。

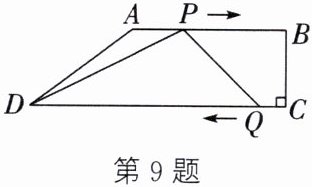
9. 如图，在四边形$ABCD$中，$AB// CD$，$\angle C = 90^{\circ}$，$AB = 6\mathrm{cm}$，$CD = 10\mathrm{cm}$，$AD = 5\mathrm{cm}$，动点$P$、$Q$分别从点$A$、$C$同时出发，点$P$以$2\mathrm{cm}/\mathrm{s}$的速度向点$B$运动，点$Q$以$1\mathrm{cm}/\mathrm{s}$的速度向点$D$运动，当一个动点到达终点时，另一个动点也立即停止运动，连接$PQ$。
（1）经过几秒，点$P$、$Q$之间的距离为$5\mathrm{cm}$？
（2）连接$PD$，是否存在某一时刻，使得$PD$恰好平分$\angle APQ$？若存在，请求出此时的运动时间；若不存在，请说明理由。

答案： （1）
过点$A$作$AE \perp CD$于$E$，则$DE=CD-AB=4\,cm$，在$Rt\triangle ADE$中，$AE=\sqrt{AD^2-DE^2}=3\,cm$。
以$C$为原点建立坐标系：$C(0,0)$，$D(10,0)$，$B(0,3)$，$A(6,3)$。
设运动时间为$t\,s(0 \leq t \leq 3)$，则$P(6-2t,3)$，$Q(t,0)$。
由$PQ=5\,cm$，得：
$\sqrt{(6-2t-t)^2+(3-0)^2}=5$
平方化简：$(6-3t)^2=16$，解得$t=\frac{2}{3}$或$t=\frac{10}{3}$（舍，$\frac{10}{3}＞3$）。
答案：$\frac{2}{3}\,s$
（2）
假设存在$t$使$PD$平分$\angle APQ$，则点$D$到$AP$和$PQ$的距离相等。
$AP$在直线$y=3$上，$D(10,0)$到$AP$距离为$3\,cm$。
直线$PQ$：$x-(2-t)y-t=0$，$D$到$PQ$距离：
$\frac{|10-t|}{\sqrt{1+(2-t)^2}}=3$
平方化简：$8t^2-16t-55=0$，解得$t=\frac{4\pm3\sqrt{14}}{4}$，均超出$t \in [0,3]$。
答案：不存在
（1）$\boxed{\dfrac{2}{3}}$
（2）$\boxed{不存在}$