《2025年通成学典课时作业本九年级数学上册苏科版苏州专版》

1. 如图，从一块直径是 2 的圆形铁片上剪出一个圆心角为 $ 90 ^ { \circ } $ 的扇形，将剪下来的扇形围成一个圆锥的侧面，那么这个圆锥的底面圆的半径是()

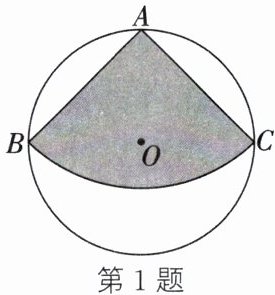
A.$ \frac { \pi } { 4 } $
B.$ \frac { \sqrt { 2 } } { 4 } $
C.$ \frac { 1 } { 2 } $
D.1

答案： B

2. (2023·娄底改编)如图，在 $ \mathrm { Rt } \triangle A B C $ 中，$ A C = 5 \mathrm { cm } $，$ B C = 12 \mathrm { cm } $，$ \angle A C B = 90 ^ { \circ } $。把 $ \mathrm { Rt } \triangle A B C $ 沿 $ B C $ 所在的直线旋转一周得到一个几何体，则这个几何体的侧面积为()

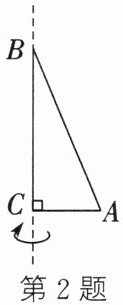
A.$ 60 \pi \mathrm { cm } ^ { 2 } $
B.$ 65 \pi \mathrm { cm } ^ { 2 } $
C.$ 120 \pi \mathrm { cm } ^ { 2 } $
D.$ 130 \pi \mathrm { cm } ^ { 2 } $

答案： B

3. (2025·苏州期末)圆锥的底面圆半径是 4，母线长是 6，则这个圆锥的侧面积为。

答案： $24\pi$

4. (1)(2024·宿迁)已知圆锥的底面圆半径为 3，母线长为 12，则其侧面展开扇形的圆心角的度数为$ ^ { \circ } $；
(2)(2024·徐州)将圆锥的侧面沿一条母线剪开后展平，所得扇形的面积为 $ 4 \pi \mathrm { cm } ^ { 2 } $，圆心角 $ \theta $ 为 $ 90 ^ { \circ } $，圆锥的底面圆的半径为$ \mathrm { cm } $。

答案：
(1)$90$；
(2)$1$。

5. 已知某圆锥的侧面积是底面积的 2 倍，求该圆锥的侧面展开图所对应的扇形的圆心角的度数。

答案： 设圆锥的底面半径为 $r$，母线长为 $R$，侧面展开图所对应的扇形的圆心角的度数为 $n{°}$。
根据题意，圆锥的侧面积是底面积的2倍，即：
$\pi rR = 2\pi r^{2}$，
化简得：
$R = 2r$，
圆锥侧面展开图所对应的扇形的弧长等于圆锥底面的周长，即：
$2\pi r = \frac{n\pi R}{180}$，
将 $R = 2r$ 代入上式，得：
$2\pi r = \frac{n\pi \cdot 2r}{180}$，
化简得：
$n = 180$。
故该圆锥的侧面展开图所对应的扇形的圆心角的度数为 $180{°}$。

6. (新情境·现实生活)(2023·赤峰)某班学生表演课本剧，要制作一顶圆锥形的小丑帽。该圆锥的底面圆的周长为 $ 20 \pi \mathrm { cm } $，母线长为 $ 30 \mathrm { cm } $。为了使帽子更美观，要粘贴彩带进行装饰，其中需要粘贴一条从底面圆周上的点 $ A $ 处开始，绕侧面一周又回到点 $ A $ 的彩带(彩带宽度忽略不计)，这条彩带的最短长度是()

A.$ 30 \mathrm { cm } $
B.$ 30 \sqrt { 3 } \mathrm { cm } $
C.$ 60 \mathrm { cm } $
D.$ 20 \pi \mathrm { cm } $

答案： B

7. (2023·济宁)如图所示为一个几何体的三视图，则这个几何体的表面积是()

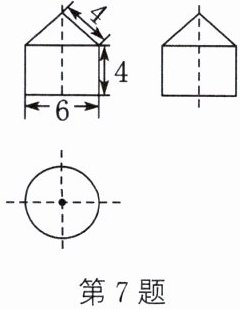
A.$ 39 \pi $
B.$ 45 \pi $
C.$ 48 \pi $
D.$ 54 \pi $

答案： C