《2025年通成学典课时作业本九年级数学上册苏科版苏州专版》

1. 在$□ ABCD$中，$AB = 10$，$BC = 14$，$E$、$F$分别为边$BC$、$AD$上的点。若四边形$AECF$为正方形，则$AE$的长为()

A.7
B.4或10
C.5或9
D.6或8

答案： D

2. 如图，小明同学用长$11\mathrm{cm}$、宽$7\mathrm{cm}$的矩形纸板制作一个底面积为$21\mathrm{cm}^2$的无盖长方体纸盒，他将纸板的四个角各剪去一个同样大小的正方形，将四周向上折起即可(损耗不计)。设剪去的正方形的边长为$x\mathrm{cm}$，则可列出关于$x$的方程为(不必化简)。

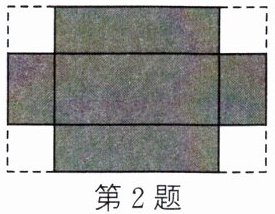
答案： $(11-2x)(7-2x)=21$。

3.(教材P30习题1.4第5题变式)(2023·鸡西)如图，在长为$100\mathrm{m}$、宽为$50\mathrm{m}$的矩形空地上修筑四条宽度相等的小路。若余下的部分全部种上花卉，且花圃的面积是$3600\mathrm{m}^2$，则小路的宽度为$\mathrm{m}$。

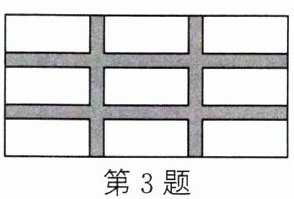
答案： 5

4.（2025·张家港期末）某社区为了解决停车难的问题，计划将一块矩形空地$ABCD$改建成一个小型停车场，其中涂色部分为停车位区域，其余部分均为宽度是$x\mathrm{m}$的道路（如图）。已知$AD = 50\mathrm{m}$，$AB = 32\mathrm{m}$，且停车位区域的面积为$880\mathrm{m}^2$，求道路的宽度。

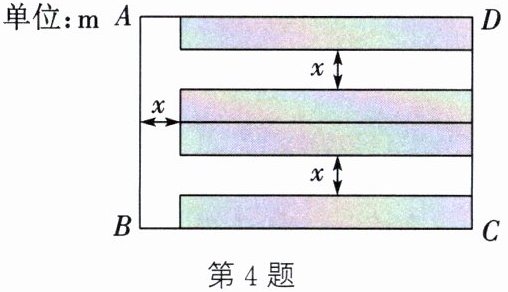
答案： 解：矩形ABCD的面积为$AD × AB = 50 × 32 = 1600 \, m^2$。
设道路宽度为$x \, m$，则停车位区域为矩形，其长为$(50 - 2x) \, m$（左右两侧道路各宽$x$），宽为$(32 - 2x) \, m$（上下两侧道路各宽$x$）。
停车位面积为$(50 - 2x)(32 - 2x) = 880$。
展开并整理方程：
$(50 - 2x)(32 - 2x) = 880$
$1600 - 100x - 64x + 4x^2 = 880$
$4x^2 - 164x + 720 = 0$
两边同除以4：
$x^2 - 41x + 180 = 0$
解方程：
判别式$\Delta = 41^2 - 4 × 1 × 180 = 1681 - 720 = 961 = 31^2$
$x = \frac{41 \pm 31}{2}$
解得$x_1 = \frac{41 + 31}{2} = 36$（不合题意，舍去，因为$32 - 2x = 32 - 72 = -40 ＜ 0$），$x_2 = \frac{41 - 31}{2} = 5$。
答：道路的宽度为$5 \, m$。

5. 用一根长为$40\mathrm{cm}$的绳子围成一个面积为$a\mathrm{cm}^2$的矩形，则$a$的值不可能为()

A.20
B.40
C.100
D.120

答案： D

6.(2024·通辽)如图，小程的爸爸用一段$10\mathrm{m}$长的铁丝网围成一个一边靠墙(墙长$5.5\mathrm{m}$)的矩形鸭舍，其面积为$15\mathrm{m}^2$，在鸭舍侧面中间位置留一个$1\mathrm{m}$宽的门(由其他材料制成)，则$BC$的长为()

A.$5\mathrm{m}$或$6\mathrm{m}$
B.$2.5\mathrm{m}$或$3\mathrm{m}$
C.$5\mathrm{m}$
D.$3\mathrm{m}$

答案： C