第4页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
1. 将一元二次方程$-3x^{2}-2=-4x$化成一般形式$ax^{2}+bx+c = 0(a>0)$后,一次项和常数项分别是()
A.$-4$、$2$
B.$-4x$、$2$
C.$4x$、$-2$
D.$3x^{2}$、$2$
A.$-4$、$2$
B.$-4x$、$2$
C.$4x$、$-2$
D.$3x^{2}$、$2$
答案:
B
2. (2024·苏州期末)已知关于$x$的一元二次方程$x^{2}+mx - 6 = 0$的一个根是$2$,则$m$的值为()
A.$3$
B.$-3$
C.$1$
D.$-1$
A.$3$
B.$-3$
C.$1$
D.$-1$
答案:
C
3. (新情境·生态环境)(2023·哈尔滨)为了改善居民的生活环境,某小区对一块矩形空地进行绿化,这块矩形空地的长比宽长$6m$,面积为$720m^{2}$。设矩形空地的长为$x m$,根据题意,可列出方程为。
答案:
$x(x - 6) = 720$
4. 有下列方程:①$2x^{2}-x+\frac{3}{x}=0$;②$(x - 2)^{2}=2x(x - 2)$;③$cx^{2}+bx+a = 0$;④$(x - 1)(2x + 3)=0$;⑤$mx^{2}-3x + 5 = 2x^{2}(m\neq0)$。其中,一定属于一元二次方程的是(填序号)。
答案:
②④(按照题目要求填序号对应的填空答案的格式应为单独的序号,由于是填多个,故按照题目特殊要求“(填序号)”以连续序号形式给出)
5. (2023·枣庄)若$x = 3$是关于$x$的方程$ax^{2}-bx - 6 = 0$的解,则$2023 - 6a + 2b$的值为。
答案:
2019(填具体数字,根据题目要求此处应填数值而非选项,若为选择题则根据选项对应选择)
6. 用方程描述下列问题中的数量关系(不用求解):
(1)已知两个连续奇数的平方和为$74$,求这两个奇数。
(2)(2024·重庆B卷)重庆在低空经济领域实现了新的突破,今年第一季度低空飞行航线安全运行了$200$架次,预计第三季度低空飞行航线安全运行将达到$401$架次。求第二、第三两个季度安全运行架次的平均增长率。
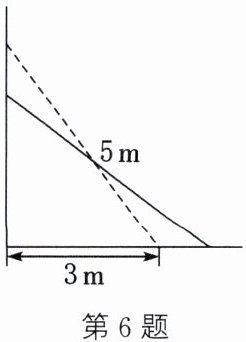
(3)如图,一架$5m$长的梯子斜靠在墙上,梯子的底端与墙的距离是$3m$。如果梯子底端向右滑动的距离与梯子顶端向下滑动的距离相等,求该梯子底端滑动的距离。
(1)已知两个连续奇数的平方和为$74$,求这两个奇数。
(2)(2024·重庆B卷)重庆在低空经济领域实现了新的突破,今年第一季度低空飞行航线安全运行了$200$架次,预计第三季度低空飞行航线安全运行将达到$401$架次。求第二、第三两个季度安全运行架次的平均增长率。
(3)如图,一架$5m$长的梯子斜靠在墙上,梯子的底端与墙的距离是$3m$。如果梯子底端向右滑动的距离与梯子顶端向下滑动的距离相等,求该梯子底端滑动的距离。

答案:
(1)设较小的奇数为$x$,则另一个奇数为$x+2$,方程为$x^{2}+(x+2)^{2}=74$。
(2)设平均增长率为$x$,方程为$200(1+x)^{2}=401$。
(3)设梯子底端滑动的距离为$x\ m$,方程为$(3+x)^{2}+(4-x)^{2}=5^{2}$。
(2)设平均增长率为$x$,方程为$200(1+x)^{2}=401$。
(3)设梯子底端滑动的距离为$x\ m$,方程为$(3+x)^{2}+(4-x)^{2}=5^{2}$。
查看更多完整答案,请扫码查看


